Принимается, что при небольших изменениях порового давления пористость и проницаемость среды, а также плотность жидкости линейно зависят от 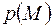 , т. е.
, т. е.
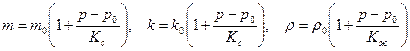
| (2.31) |
где 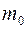 ,
, 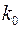 и
и 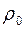 – соответственно пористость, проницаемость и плотность при начальном давлении
– соответственно пористость, проницаемость и плотность при начальном давлении 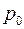 ;
; 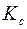 и
и 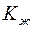 – соответственно модули объемной упругости скелета и жидкости. Кроме того, принимаем, что
– соответственно модули объемной упругости скелета и жидкости. Кроме того, принимаем, что 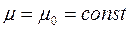 .
.
К уравнениям (2.30 и (2.31) необходимо присоединить еще уравнение неразрывности движения жидкости (2.22), которое в силу неполного, равного 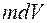 , заполнения элементарного объема
, заполнения элементарного объема 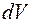 сплошной среды принимает вид
сплошной среды принимает вид
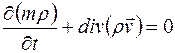 . .
| (2.32) |
Уравнения (2.30) – (2.32) образуют, таким образом, замкнутую систему для определения функций 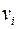 ,
, 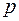 ,
, 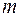 и
и 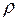 . Но если подставить уравнения (2.30) и (2.31) в (2.32) и учесть, что в реальных ситуациях величины
. Но если подставить уравнения (2.30) и (2.31) в (2.32) и учесть, что в реальных ситуациях величины 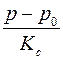 и
и 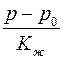 много меньше единицы, то отбросив малые величины высших порядков, получим одно основное
много меньше единицы, то отбросив малые величины высших порядков, получим одно основное
классическое уравнение теории фильтрации:
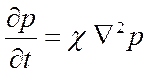 , ,
| (2.33) |
где 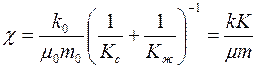 – коэффициент пьезопроводности среды;
– коэффициент пьезопроводности среды;
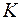 – приведенный модуль объемной упругости среды;
– приведенный модуль объемной упругости среды; 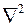 – оператор Лапласа. Пьезопроводность
– оператор Лапласа. Пьезопроводность 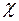 имеет размерность м2/с.
имеет размерность м2/с.
Если 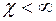
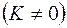 , то уравнение (2.33) описывает нестационарное поле давления при упругом режиме фильтрации. При
, то уравнение (2.33) описывает нестационарное поле давления при упругом режиме фильтрации. При 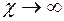
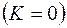 имеем уравнение Лапласа
имеем уравнение Лапласа
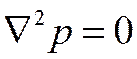 , ,
| (2.34) |
которое характеризует неупругий (жесткий) режим фильтрации и, следовательно, стационарное поле давления. Это же уравнение имеет место при 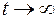 , т. е. при установившемся режиме фильтрации.
, т. е. при установившемся режиме фильтрации.
Для однозначного определения поля давления 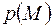 в заданной области
в заданной области 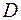 , ограниченной поверхностью
, ограниченной поверхностью 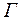 , необходимо и достаточно, чтобы решение уравнения (2.33) удовлетворяло начальному условию (при
, необходимо и достаточно, чтобы решение уравнения (2.33) удовлетворяло начальному условию (при 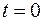 )
)
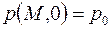 при при 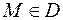
| (2.35) |
и при 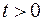 граничным условиям:
граничным условиям:
если на поверхности 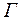 (или ее части) задано давление
(или ее части) задано давление 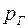 , то
, то
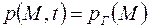 при при 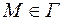 , ,
| (2.36) |
если задана нормальная составляющая скорости фильтрации, то
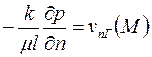 , ,
| (2.37) |
если поверхность 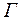 покрыта тонкой слабопроницаемой перемычкой (например, глинистая корка на стенке скважины), то
покрыта тонкой слабопроницаемой перемычкой (например, глинистая корка на стенке скважины), то
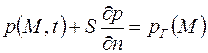 , ,
| (2.38) |
где 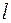 – характерный линейный размер;
– характерный линейный размер; 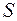 – коэффициент поверхностного фильтрационного сопротивления, получивший название параметр «скин-эффекта».
– коэффициент поверхностного фильтрационного сопротивления, получивший название параметр «скин-эффекта».
Ясно, что для уравнения (2.34) начальное условие (2.35) смысла не имеет, а граничные условия вида (2.36) – (2.38) сохраняются.
2. Модель ламинарной фильтрации ньютоновских однородных жидкостей д ля анизотропной среды.
 2015-03-08
2015-03-08 362
362








