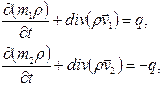
| (2.48) |
где индексами 1 и 2 обозначены величины, характеризующие соответственно систему трещин и пор;
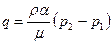 . .
| (2.49) |
– интенсивность перетока жидкости между этими системами; 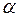 – новая безразмерная величина, характеризующая данную среду.
– новая безразмерная величина, характеризующая данную среду.
При этом пористости 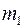 и
и 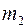 являются функциями обоих давлений, т.е.
являются функциями обоих давлений, т.е.
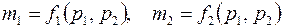 . .
| (2.50) |
Однако во многих случаях систему уравнений (2.47) – (2.48) можно упростить, если исходить из следующих условий:
а) объем, занимаемый трещинами, много меньше объема пор, т.е. допустимо принять 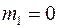 ;
;
б) изменение пористости 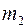 происходит в основном за счет изменения порового давления
происходит в основном за счет изменения порового давления 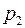 и поэтому при небольших изменениях этого давления
и поэтому при небольших изменениях этого давления
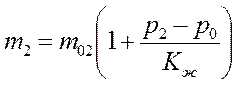 ; ;
| (2.51) |
в) проницаемость 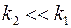 , т.е. фильтрацией в порах можно пренебречь
, т.е. фильтрацией в порах можно пренебречь 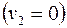 ;
;
г) жидкость слабосжимаема так что
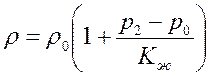 , ,
| (2.52) |
где 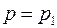 или
или 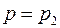 в зависимости от того, рассматривается жидкость в трещинах или в порах;
в зависимости от того, рассматривается жидкость в трещинах или в порах;
д) вязкость жидкости 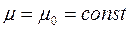 .
.
Физическая сущность перечисленных допущений состоит в том, что в системе трещины – поры рассматривается фильтрация жидкости по трещинам в условиях интенсивного массобмена с жидкостью, находящейся в упругом деформированном поровом пространстве.
В результате принятых упрощений уравнения (2.48) примут вид
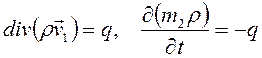 . .
|
Подставляя сюда соотношения (2.47), (2.49), (2.51), (2.52) и отбрасывая малые величины высших порядков, получим
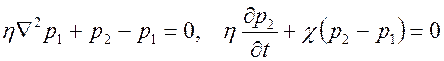 , ,
| (2.53) |
где 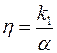 – специфическая характеристика трещиновато-пористой среды;
– специфическая характеристика трещиновато-пористой среды; 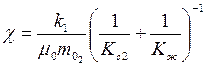 – своеобразная пьезопроводность среды.
– своеобразная пьезопроводность среды.
Параметр 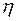 имеет размерность площади, и для реальных пород его порядок может изменяться в широких пределах – от 10-1 до 106 м2.
имеет размерность площади, и для реальных пород его порядок может изменяться в широких пределах – от 10-1 до 106 м2.
Легко заметить, что путем исключения одного из давлений система уравнений (2.53) сводится к одному уравнению
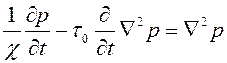 , ,
| (2.54) |
где 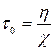 – параметр, называемый временем запаздывания.
– параметр, называемый временем запаздывания.
Это уравнение отличается от классического уравнения (2.33) слагаемым, содержащим параметр 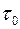 . В пределе, когда
. В пределе, когда 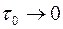 , среда с двойной пористостью переходит в чисто пористую и уравнения (2.54) и (2.33) совпадают.
, среда с двойной пористостью переходит в чисто пористую и уравнения (2.54) и (2.33) совпадают.
При жестком режиме фильтрации 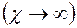 или при установившейся фильтрации
или при установившейся фильтрации 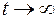 уравнение (2.54) обращается в уравнение Лапласа (2.34).
уравнение (2.54) обращается в уравнение Лапласа (2.34).
Следовательно, ставить задачу о фильтрации жидкости в трещиновато-пористой среде имеет смысл при 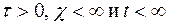 .
.
Начальное и граничные условия, которые необходимо присоединить к уравнению (2.54), обладают некоторой особенностью. Прежде всего ясно, что граничную задачу, связанную с уравнением (2.54) следует рассматривать относительно одного из давлений – 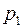 или
или 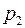 .
.
Если начальные условия 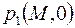 и
и 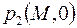 удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления
удовлетворяют первому уравнению (2.53), то задачу целесообразно решать относительно давления 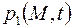 , принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления
, принимая начальные и граничные условия в виде выражений (2.35) – (2.38). После определения давления 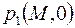 вычисляют поровое давление
вычисляют поровое давление 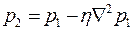 .
.
В противном случае задачу следует решать относительно давления 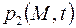 . Но здесь имеет место определенная специфика в задании граничных условий.
. Но здесь имеет место определенная специфика в задании граничных условий.
Если начальное распределение давления 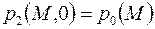 согласовано с граничными условиями
согласовано с граничными условиями 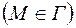 вида
вида
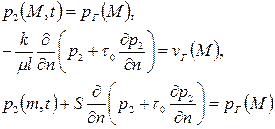 , ,
| (2.55) |
при 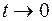 , то в таком виде граничная задача и рассматривается.
, то в таком виде граничная задача и рассматривается.
Но если же согласования нет, то к правым частям соответствующих граничных условий необходимо прибавить слагаемое 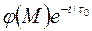 , где
, где 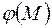 – невязка существующего граничного условия:
– невязка существующего граничного условия:
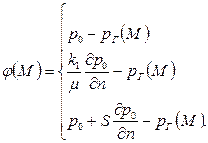
| (2.56) |
Это свидетельствует о том, что заданный скачок граничных условий в порах трещиновато-пористой среды не уничтожается мгновенно, как в обычной пористой среде, а убывает по закону 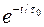 . Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений
. Такое качественное отличие – результат принятого упрощения пренебрежения фильтрацией жидкости в порах, где давление изменяется только благодаря массообмену с жидкостью в трещинах. Аналогично, предположение о жестком характере фильтрации жидкости в трещинах приводит к указанной выше проверке начальных распределений давлений 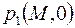 и
и 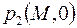 .
.
После решения граничной задачи относительно порового давления 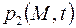 распределение давления
распределение давления 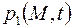 в трещинах определяется по формуле (2.53)
в трещинах определяется по формуле (2.53)
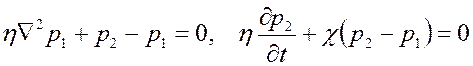
 2015-03-08
2015-03-08 402
402








