Встречаемые на практике отношения могут обладать или не обладать свойствами рефлексивности, антирефлексивности, симметричности, антисимметричности, полнотой (линейности), транзитивности. Некоторые устойчивые комбинации встречаются очень часто. Они заслуживают внимания и изучения.
Определение 3.1. Рефлексивное, симметричное, транзитивное отношение называют отношением эквивалентности (R, ↔, ≡).
Примеры отношений эквивалентности:
1. Отношение "... Имеет тот же возраст, что и..." на множестве всех людей. “эквивалентные” люди принадлежат к одной и той же возрастной группе.
2. Если у людей глаза одинакового цвета, то эквивалентны, в отношении цвета глаз.
3. Отношение “... Имеет те же углы что...” на множестве всех треугольников Очевидно, треугольники эквивалентны тогда и только тогда когда они подобны.
4. Отношение R заданное условием x R y, если только xy >0 на множестве ненулевых целых чисел является отношением эквивалентности. При этом эквивалентные числа имеют одинаковый знак.
Определение 3.2. Подмножество элементов множества M, эквивалентных x, называют классом эквивалентности для x {x}≡↔{y|yÎM & y≡x}
Отношение эквивалентности имеет важную особенность: эквивалентность R разбивает множество М, на котором оно задано, на непересекающиеся подмножества так, что элементы одного и того же подмножества находятся в отношении R, а между элементами из разных подмножеств отношение R отсутствует. В таком случае говорят, что отношение R задает разбиение на множестве М, или систему классов эквивалентности по отношению R. Мощность этой системы называется индексом разбиения.
Теорема 3.1: всякое отношение эквивалентности на множестве M определяет разбиение на множестве M, причем среди элементов разбиения нет пустых.
Обратная теорема 3.1*: всякое разбиение на множестве M, не содержащее пустых элементов, определяет отношение эквивалентности на множестве M.
Определение 3.3. Множество классов эквивалентности множествах по отношению ρ называется фактор-множеством множества М по отношению ρ и обозначается [ Х/ρ ].
Определение 3.4. Бинарное отношение a на множестве X называется отношением порядка (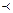 ), если оно транзитивно:
), если оно транзитивно:
" а,b,с Î А, аRb & bRс Þ аRс
и антисимметрично:
" а,b Î А, аRb & bRа Þ a = b
Пример. Рассмотрим отношение "старше" на множестве людей. Очевидно, что оно транзитивно и антисимметрично, и, следовательно, является отношением порядка.
Определение 3.5. Множество X с определенным на нем отношением порядка α называется упорядоченным множеством и обозначается <X; α>.
Упорядоченное множество <M; α> с небольшим числом элементов наглядно представляется ориентированным графом. При этом элементам множества M сопоставляются вершины графа (обозначаются на рисунке точками), а элементам отношения α - дуги (линии со стрелками).
Так, например, на рисунке 3.1 приведен ориентированный граф, представляющий отношение α= {(a, a), (a, b), (a, c), (b, c)} на множестве M = { a, b, c, d }.
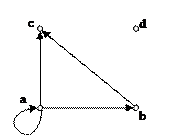
Рис. 3.1. Граф упорядоченного множества
Задать порядок на множестве можно различными способами. Так, например, на рисунке 3.2 приведено три способа упорядочения четырех стран.
| Площадь | Россия | США | Франция | Англия |
| Население | США | Россия | Франция | Англия |
| Плотность населения | Англия | Франция | США | Россия |
Рис. 3.2. Три способа упорядочения
На рисунке 3.3 приведены ориентированные графы, представляющие отношения "делится" и "меньше" на множестве M = { 1, 2, 3, 4 } натуральных чисел.



Рис. 3.3. Графы отношений "делится" (а) и "меньше" (б) на множестве { 1, 2, 3, 4 }
Разновидности отношений порядка
Определение 3.6. Отношение порядка α называется отношением нестрогого порядка на множестве X, если α рефлексивно:
(" a Î X)(a α a).
Отношение нестрогого порядка обычно обозначается символом ≤. Если x ≤ y, то говорят, что "элемент x предшествует элементу y " или " y следует за x ".
Пример. Отношение x ≤ y на множестве действительных чисел является отношением нестрогого порядка.
Пример 1*. Отношение m|n (m делит n) на произвольном подмножестве натуральных чисел является нестрогим порядком. На рисунке 3.4 приведен граф, соответствующий упорядоченному множеству <{2, 3, 6, 7, 14},|>.
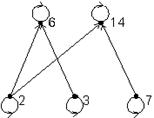
Рис. 3.4. Граф нестрого упорядоченного множества
Пример. Тождественное отношение является как отношением эквивалентности, так и отношением нестрогого порядка.
Определение 3.7. Два элемента x, y Î X называются сравнимыми элементами упорядоченного множества X, если либо x α y, либо y α x.
Например: Несравнимыми элементами в упорядоченном множестве из примера 1* являются элементы 7 и 2, 2 и 3, 3 и 7.
Определение 3.8. Отношение порядка α называется отношением строгого порядка на множестве X, если α антирефлексивно:
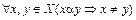 .
.
Отношение строгого порядка обозначается символом <.
Пример. Пусть f и g – функции с одинаковыми областями определения. Определим отношение > следующим образом: f > g, если для любого x из области определения функции f (x) > g (x). Очевидно, что данное отношение является отношением строгого порядка.
Для функций f и g, изображенных на рисунке 3.5, имеет место соотношение f > g. Пары функций f и h, а также g и h несравнимы.
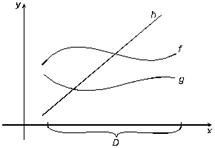
Рис. 3.5. Три функции
Пример. Алфавитный порядок является отношением строгого порядка на множестве букв.
Пример. Пусть на множестве X задано отношение строго порядка α. Как можно задать отношение строгого порядка на множестве X ´ X, то есть, как сравнивать пары элементов из множества X? Один из возможных вариантов состоит в следующем. На множестве X определим отношение b условием:
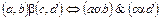 .
.
Отношение b является строгим порядком.
Пример. Другой способ задания строгого порядка на множестве X ´ X состоит в следующем. Будем считать, что выполнено соотношение (a, b)γ(c, d), если
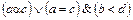 .
.
Это отношение порядка называется лексикографическим. В общем случае оно определяется следующим образом. Для слов v и w одинаковой длины полагается v < w, если существует такой номер k, что v 1= w 1, v 2= w 2, …, v k-1= w k-1, v k= w k, где v i, w i – i -ые буквы слов v и w соответственно. Для слов v = v 1 v 2… v n и w = w 1 w 2… w n w n+1… w n+k (k > 0) разной длины считается v < w, если v 1 v 2… v n< w 1 w 2… w n или v 1 v 2… v n= w 1 w 2… w n, и w < v, если w 1 w 2… w n< v 1 v 2… v n. Такой способ упорядочения используется в словарях. В этом порядке, например:
детство < отрочество < юность,
институт < школа < ясли,
12 < 123 < 4.
Как уже отмечалось, упорядоченные множества удобно изображать в виде графов. При этом если α – отношение строго порядка, то граф отношения α не содержит циклов. Верно и обратное: для любого графа G без циклов существует отношение α строгого порядка такое, что граф, ассоциированный с данным отношением, совпадает с транзитивным замыканием графа G. (Транзитивным замыканием графа G называется граф, полученный из графа G добавлением дуг, связывающих каждую вершину α с вершинами, достижимыми из α.) Действительно, пусть G – граф без контуров. Определим на множестве M вершин этого графа отношение α: x α y, если существует путь по направлению дуг, ведущий из x в y. Легко видеть, что ввиду отсутствия циклов отношение α является строгим порядком.
Определение 3.9. Множество X с бинарным отношением α называется связным, если для любых двух различных элементов x и y из X либо x α y, либо y α x.
Определение 3.10. Связное отношение порядка на множестве X называется отношением линейного порядка.
Пример. Лексикографический порядок слов в словаре является линейным порядком.
Пример. Отношение включения на множестве фигур линейным порядком не является (рис. 3.6).
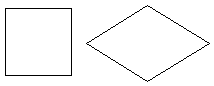
Рис. 3.6. Две несравнимые фигуры
Пример. Отношение "старше" на множестве людей является линейным порядком.
 2015-03-08
2015-03-08 2629
2629
