Основное определение

Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании

Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.

1. Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку (рис. 9.1(а)). Эта задача была решена Эйлером (1707-1783) в 1736 году.

2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 9.1(б)). Эта задача была решена Куратовским (1896-1979) в 1930 году.

3. Задача о четырех красках. Любую карту на плоскости раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом (рис. 9.1(в)).

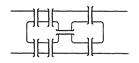
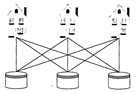
а) б) в)

Рисунок 9.1.

Определение 9.1. Графом G (V, E) называется совокупность двух множеств – непустого множества V (множества вершин) и множества E неупорядоченных пар различных элементов множества V (E – множество ребер). G (V, E)=< V, E >, V ≠Æ, E Ì V ´ V, E = E ^-1. Число вершин графа G обозначим р, а число ребер — q: p:= p (G):=| V |, q:= q (G):=| E |.

Определение 9.2. Пусть ν₁, ν₂ — вершины, e = (ν₁, ν₂) – соединяющее их ребро. Тогда вершина ν_i и ребро e инцидентны, вершина ν₂ и ребро e также инцидентны. Два ребра, инцидентные одной вершине, называются смежными, две вершины, инцидентные одному ребру, также называются смежными.