Замечание:
Теория интегральных уравнений с симметричным и действительным ядром была построена Гильбертом (1904г) с привлечением теории симметричных квадратичных форм при переходе от конечного числа переменных к бесконечному. Затем Э. Шмидт (1907г)предложил более простой метод обоснования полученных результатов. Поэтому теорию интегральных уравнений с симметричным ядром называют теорией Гильбета – Шмидта. Теория интегральных уравнений с симметричным ядром может быть построена независимо от теории Фредгольма, исходя из свойств вполне непрерывных симметричных операторов в пространстве 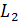
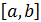 . Абстрактная теория линейных операторов в гильбертовом пространстве представляет собой один из популярных отделов функционального анализа. В последние годы методы гильбертова пространства стали инструментом, которым пользуются не только математики, но и физики.
. Абстрактная теория линейных операторов в гильбертовом пространстве представляет собой один из популярных отделов функционального анализа. В последние годы методы гильбертова пространства стали инструментом, которым пользуются не только математики, но и физики.
Многие задачи математической физики приводят к задаче определения собственных значений и собственных функций оператора и проблеме разложения произвольной функции по собственным функциям оператора.
Исследование спектра оператора и разложение заданной функции по собственным функциям носит название спектрального анализа. Один из крупнейших математиков Иоганн фон Нейман занимался вопросами математического обоснования квантовой механики.
Только при использовании идей и методов функционального анализа возможно глубокое понимание теории и получение наиболее общих результатов.
Желающие могут ознакомиться с изложением некоторых фактов из теории интегральных уравнений на основе общих положений функционального анализа по книге Краснов М.Л. «Интегральные уравнения. (Введение в теорию), изд. «Наука» 1975 г.
1. Некоторые сведения из функционального анализа.
Пространство 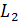
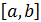 состоит из функций, интегрируемых с квадратом.
состоит из функций, интегрируемых с квадратом.
Т.е. таких, для которых: 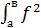 (x)dx
(x)dx 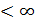 , т.е. интеграл имеет конечное значение.
, т.е. интеграл имеет конечное значение.
Этому условию удовлетворяют, например, кусочно монотонные функции на отрезке 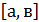 .
.
Скалярное произведение функций определяется как
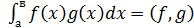 ………(1)
………(1)
Тогда: 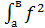 (x)dx =
(x)dx = 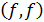 =
= 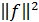 …….(2)
…….(2)
где 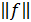 – норма функции.
– норма функции.
Если норма функции равна 1, т.е. 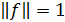 , то функцию называют нормированной.
, то функцию называют нормированной.
Для f(x) и g(x) имеет место неравенство треугольника:
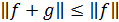 +
+ 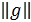
а также неравенство Коши – Буняковского:
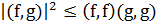
Функции f(x) и g(x) назовем ортогональными, если их скалярное произведение равно нулю (f, g) = 0.
С помощью скалярного произведения, точнее нормы, может быть введена метрика: 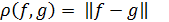 (расстояние между элементами.)
(расстояние между элементами.)
Сходимость в среднем последовательности 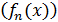 к функции f(x) в пространстве
к функции f(x) в пространстве 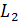
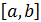 означает, что
означает, что 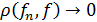 или
или
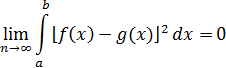
Рассмотрим ортонормированную последовательность функции из 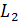
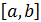
 (3)
(3)
Следовательно, функции удовлетворяют соотношению:
(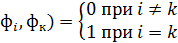
Ортогональная система называется полной, если не существует отличной от тождественного нуля квадратично суммируемой функции, ортогональной всем функциям системы. Ортогональные функции, взятые в любом конечном числе, линейно независимы.
Ряд 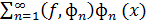 называется рядом Фурье функции f(x
называется рядом Фурье функции f(x 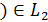
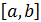 по ортонормированной системе (3).
по ортонормированной системе (3).
Числа 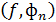 =
= 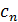 называются коэффициентами Фурье.
называются коэффициентами Фурье.
Имеет место неравенство Бесселя:
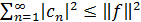 …..(4)
…..(4)
Если в формуле (4) имеет место равенство, то получаем так называемое уравнение замкнутости.
Ряд Фурье, любой квадратично суммируемой функции, сходится в среднем.
Если ортонормированная система (3) полна, то для любой квадратично суммируемой функции имеет место уравнение замкнутости, которое еще называется равенством Парсеваля.
.2. Характеристические числа и собственные функции.
Значение параметра λ, при котором однородное уравнение Фредгольма
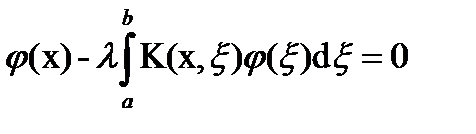 имеет решение
имеет решение 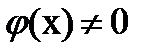 в [a, b]
в [a, b]
(нетривиальное решение), называют собственным значением (характеристическим числом) интегрального уравнения, а соответствующее решение 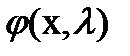 называют собственной функцией уравнения (характеристической функцией).
называют собственной функцией уравнения (характеристической функцией).
Собственные функции обладают следующими очевидными свойствами:
а) если 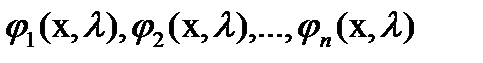 - собственные функции, то
- собственные функции, то 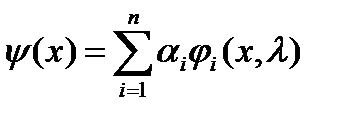 , где
, где 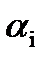 - const, также является собственной функцией, то есть интегральное уравнение может иметь бесконечное множество собственных функций, если имеет хотя бы одну собственную функцию;
- const, также является собственной функцией, то есть интегральное уравнение может иметь бесконечное множество собственных функций, если имеет хотя бы одну собственную функцию;
б) Собственные функции, соответствующие характеристическим значениям, различным между собой, линейно независимы.
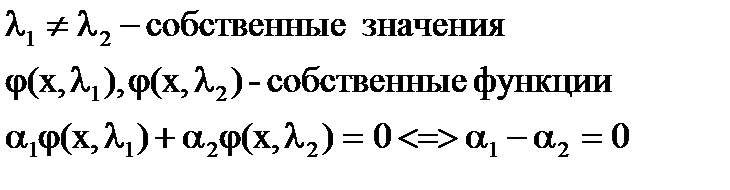
Покажем это:
Пусть 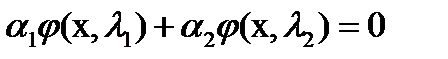 Имеем
Имеем
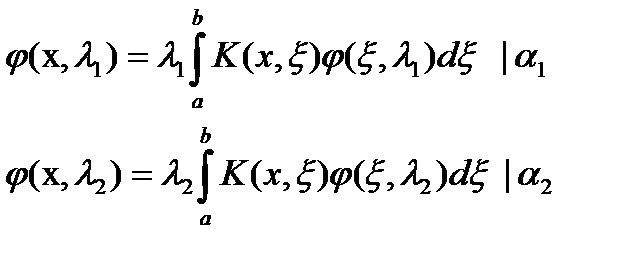
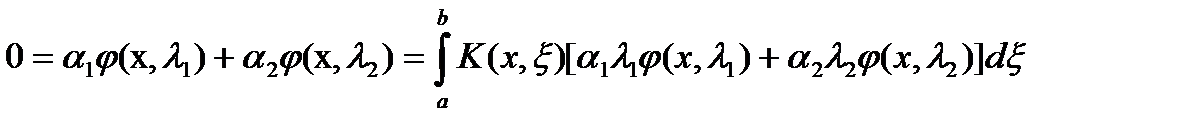
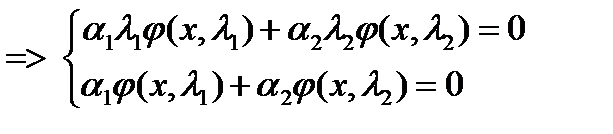
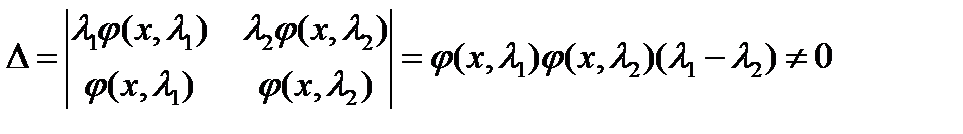
Значит, система имеет решение 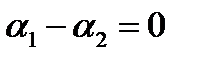 , то есть
, то есть 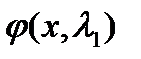 и
и 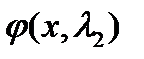 - линейно независимы.
- линейно независимы.
Назовем число m линейно независимых собственных функций рангом характеристического значения λ.
: Оператором Фредгольма называют
Kф = 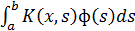 , где
, где 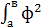 (x)dx
(x)dx 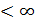 , и ядро
, и ядро
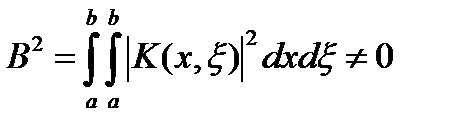
Собственным значением интегрального оператора К называется такое значение μ, при котором уравнение Кφ=μφ имеет решение φ≠0. Отсюда φ-μКφ=0 имеет решение φ≠0, если μ – собственное значение. Обозначим 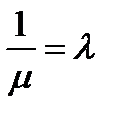 характеристическое число интегрального уравнения.
характеристическое число интегрального уравнения.
Интегральное уравнение с симметричным действительным ядром, таким, что:
К(х, s) = K(s, x).
Теория линейных и. у. с симметричным и действительным ядром была впервые построена Д. Гильбертом (1904) привлечением теории симметричных квадратичных форм с помощью перехода от конечного числа переменных к бесконечному. Затем Э. Шмидт (1907) предложил более элементарный метод обоснования результатов Д. Гильберта. Поэтому теорию часто наз. также теорией Гильберта- Шмидта. Значительное ослабление ограничений, налагаемых в этой теории на заданные и искомые элементы уравнения, было достигнуто Т. Карлеманом.
Пусть имеется и. у. 2-го рода с действительным симметричным ядром:
ф(х) -- λ 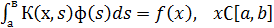 (1)
(1)
При построении теории. достаточно предполагать, что симметричное ядро К измеримо на квадрате [а, b]X[ а, b]
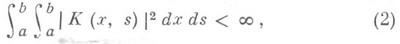
а свободный член f и искомая функция j - интегрируемые с квадратом функции на отрезке [ а, b](интегралы понимаются в смысле Лебега).
Разработка теории начинается с изучения ряда общих свойств собственных чисел и собственных функций однородного симметричного
А именно, доказывается, что:
1) все характеристические числа интегрального уравнения с симметричным ядром действительны, а собственные функций, соответствующие различным собственным значениям 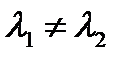 , ортогональны, то есть
, ортогональны, то есть
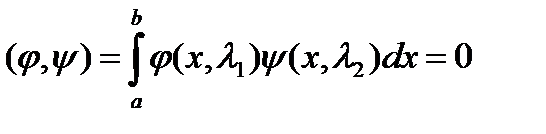
2) у интегрального уравнения с симметричным ядром существует, по крайней мере, одно собственное значение ≠0; собственные значения образуют дискретную последовательность 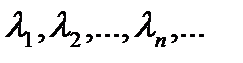 , причем в каждом конечном интервале содержится не более конечного числа собственных значений, и каждое собственное значение имеет конечный ранг.
, причем в каждом конечном интервале содержится не более конечного числа собственных значений, и каждое собственное значение имеет конечный ранг.
Множество всех собственных чисел уравнения (3) наз. спектром этого уравнения. Спектр - непустое конечное или счетное множество чисел, каждому числу спектра соответствует конечное множество линейно независимых собственных функций. Собственные числа и собственные функции можно расположить в виде последовательностей:

так, что абсолютные величины собственных чисел не убывают 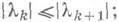 каждое собственное число повторяется столько раз, сколько собственных функций ему соответствует. Последовательности (4) наз. системой собственных чисел и собственных функций симметричного ядра Кили уравнения (3). Нахождение этой системы равносильно полному решению однородного симметричного и. у. (3).
каждое собственное число повторяется столько раз, сколько собственных функций ему соответствует. Последовательности (4) наз. системой собственных чисел и собственных функций симметричного ядра Кили уравнения (3). Нахождение этой системы равносильно полному решению однородного симметричного и. у. (3).
Ряд Фурье ядра К(х, s), рассматриваемого как функция от s относительно ортонормированной системы, будет
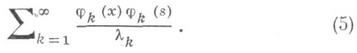
Так составленный ряд из системы собственных чисел и собственных функций симметричного ядра К наз. билинейным рядом ядра К или билинейным разложением ядра К по его собственным функциям. Этот ряд сходится в среднем к ядру К, т. е.
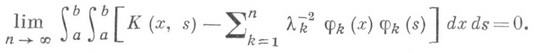
Если же билинейный ряд (5) сходится равномерно, то
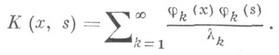
В частности, это последнее равенство всегда имеет место, если ядро обладает лишь конечным множеством собственных чисел. В этом случае ядро К является вырожденным. Имеет место и обратное утверждение: вырожденное симметричное ядро имеет конечное множество собственных чисел (и, следовательно, конечное множество собственных функций). Билинейный ряд непрерывного на квадрате ядра Кс положительными собственными числами сходится равномерно.
Зная систему (4) собственных чисел и собственных функций, можно построить решение неоднородного уравнения (1).
Если 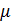 не является собственным числом ядра К, то симметричное неоднородное уравнение (1) имеет единственное решение, выражаемое формулой
не является собственным числом ядра К, то симметричное неоднородное уравнение (1) имеет единственное решение, выражаемое формулой
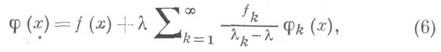
где
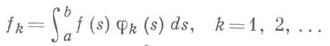 --коэффициенты Фурье для f(x)
--коэффициенты Фурье для f(x)
Пусть 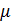 - собственное число ядра К; тогда симметричное и. у. (1) разрешимо лишь в случае, если удовлетворяются условия
- собственное число ядра К; тогда симметричное и. у. (1) разрешимо лишь в случае, если удовлетворяются условия
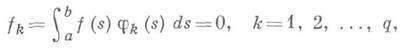
При соблюдении этих условий все решения уравнения (1) выражаются формулой
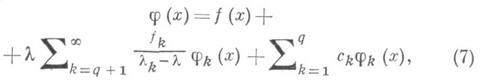
где 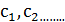 - произвольные постоянные.
- произвольные постоянные.
Если ядро К имеет бесконечное множество собственных чисел и, следовательно, в правых частях формул (6), (7) стоят бесконечные ряды, то они сходятся в среднем. Если от ядра К дополнительно потребовать, что оно удовлетворяет условию
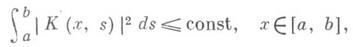
то упомянутые ряды будут сходиться абсолютно и равномерно.
Формулы (6) и (7) наз. формулами Шмидта.
Симметричное ядро наз. полным, если система его собственных функций полна (замкнута).
Теорема Пикара. Пусть К(х, s)- полное ядро. Тогда для разрешимости уравнения (8) необходимо и достаточно, чтобы ряд
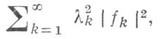
где 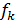 - коэффициенты Фурье функции f, сходился. При выполнении этого условия решение (единственное) представимо в виде
- коэффициенты Фурье функции f, сходился. При выполнении этого условия решение (единственное) представимо в виде
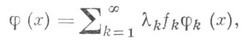
причем последний ряд сходится в среднем.
Пример.
Найти характеристические числа и собственные функции однородного уравнения.
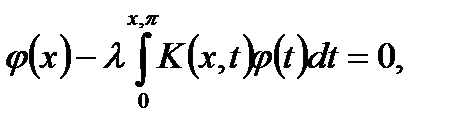 где
где
K(x, t) = 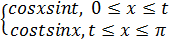
Решение: Данное уравнение представим в виде
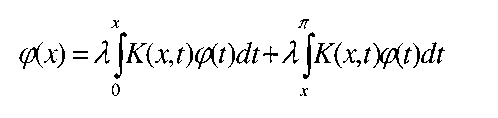
Или
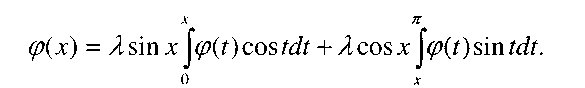
Дифференцируя обе части (1), находим
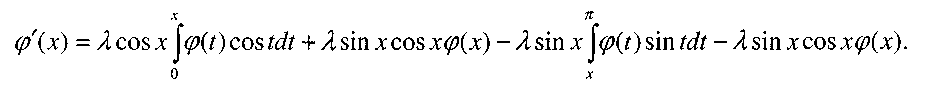
Или
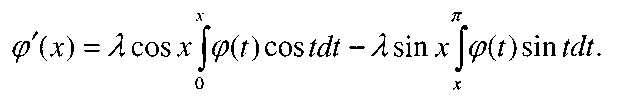 (2)
(2)
Повторное дифференцирование дает
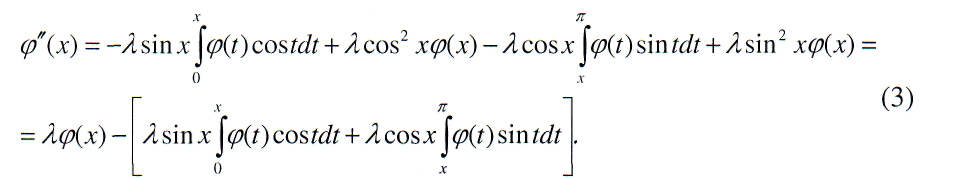
Выражение в квадратных скобках равно 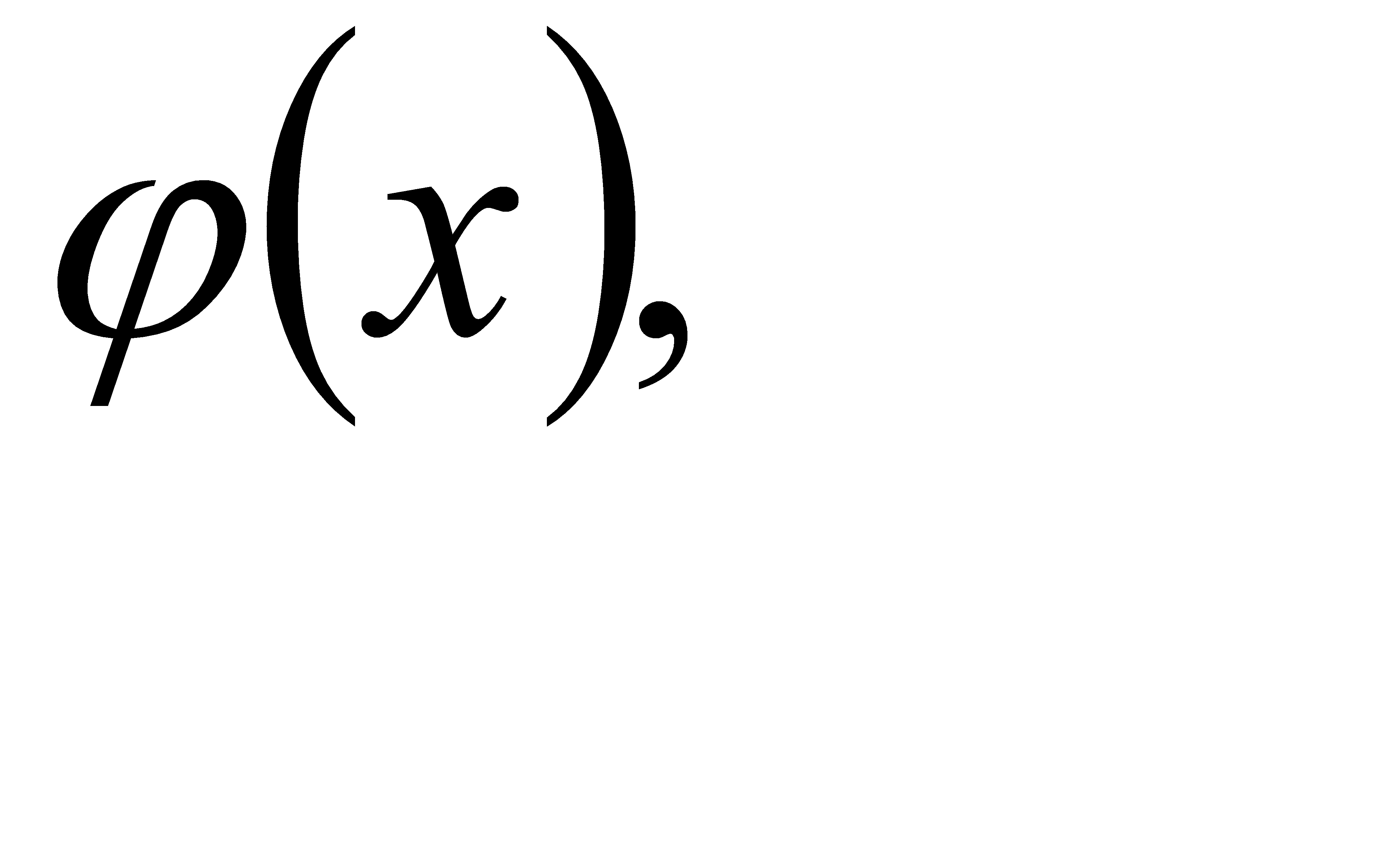 так что
так что
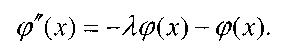
Из равенств (1) и (2) находим, что
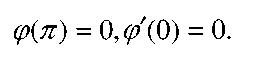
Итак, данное интегральное уравнение сводится к следующей краевой задаче:
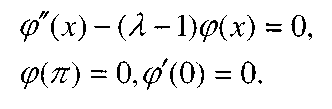
Здесь возможны три случая:
1) 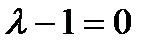 или
или 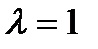 . Уравнение (3) принимает вид
. Уравнение (3) принимает вид 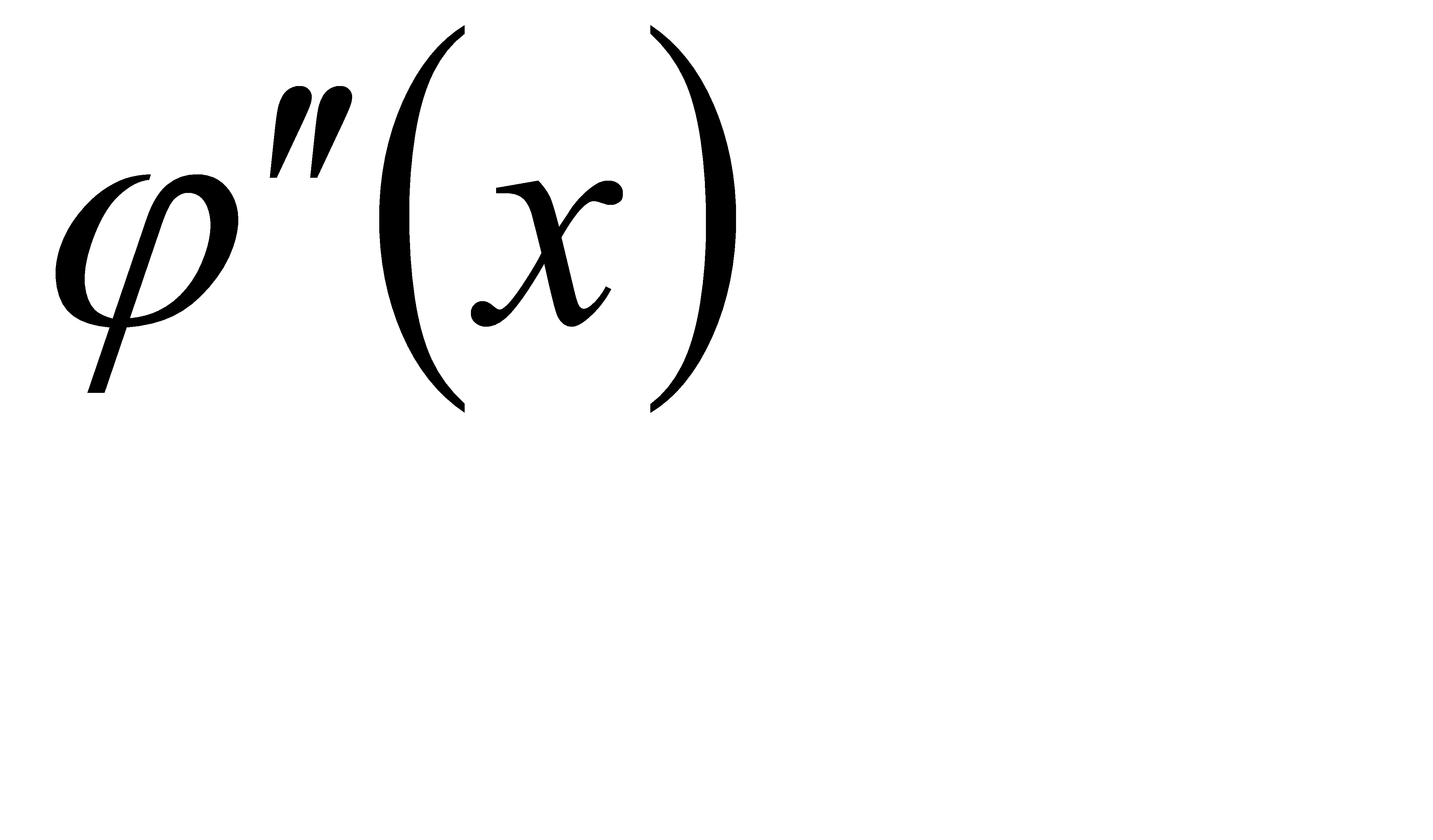 = 0. Его общее
= 0. Его общее
решение будет 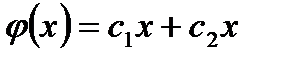 .
.
Используя краевые условия (4), получим для нахождения неизвестных 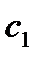 и
и 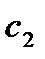 систему
систему
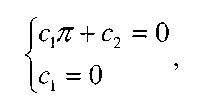
которое имеет единственное решение 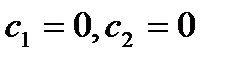 , следовательно, интегральное уравнение имеет только тривиальное решение
, следовательно, интегральное уравнение имеет только тривиальное решение
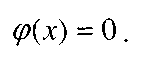
2) 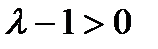 или
или 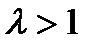 . Общее решение уравнения (3) имеет вид
. Общее решение уравнения (3) имеет вид
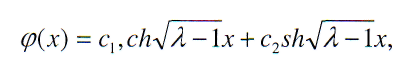
откуда
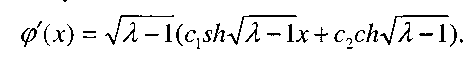
Для нахождения значений с, и с2 краевые условия дают систему
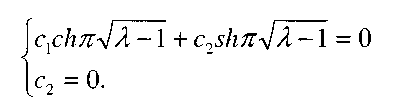
Система имеет единственное решение 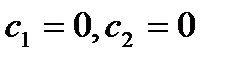 . Интегральное уравнение имеет тривиальное решение
. Интегральное уравнение имеет тривиальное решение 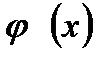 = 0. Итак, при
= 0. Итак, при 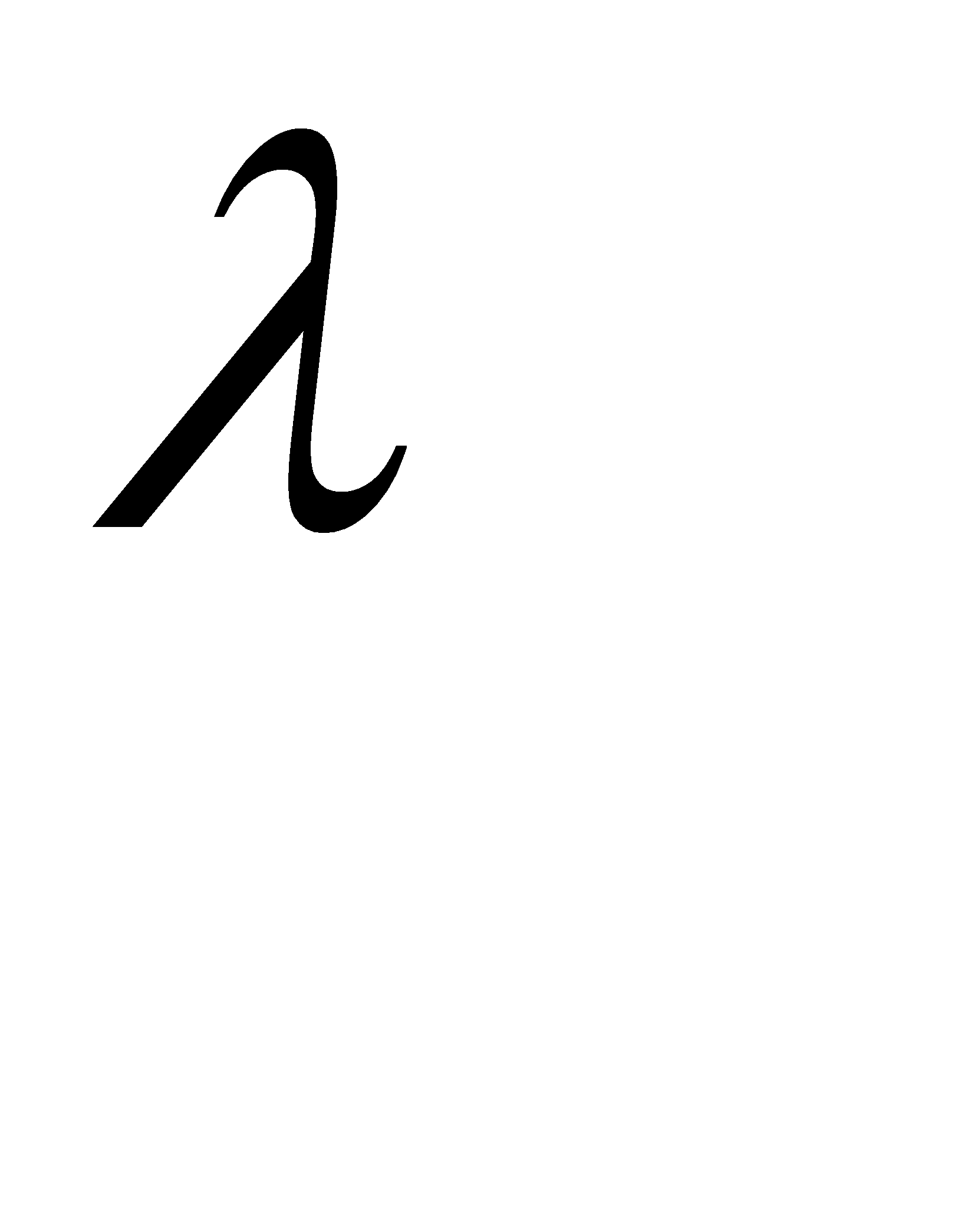
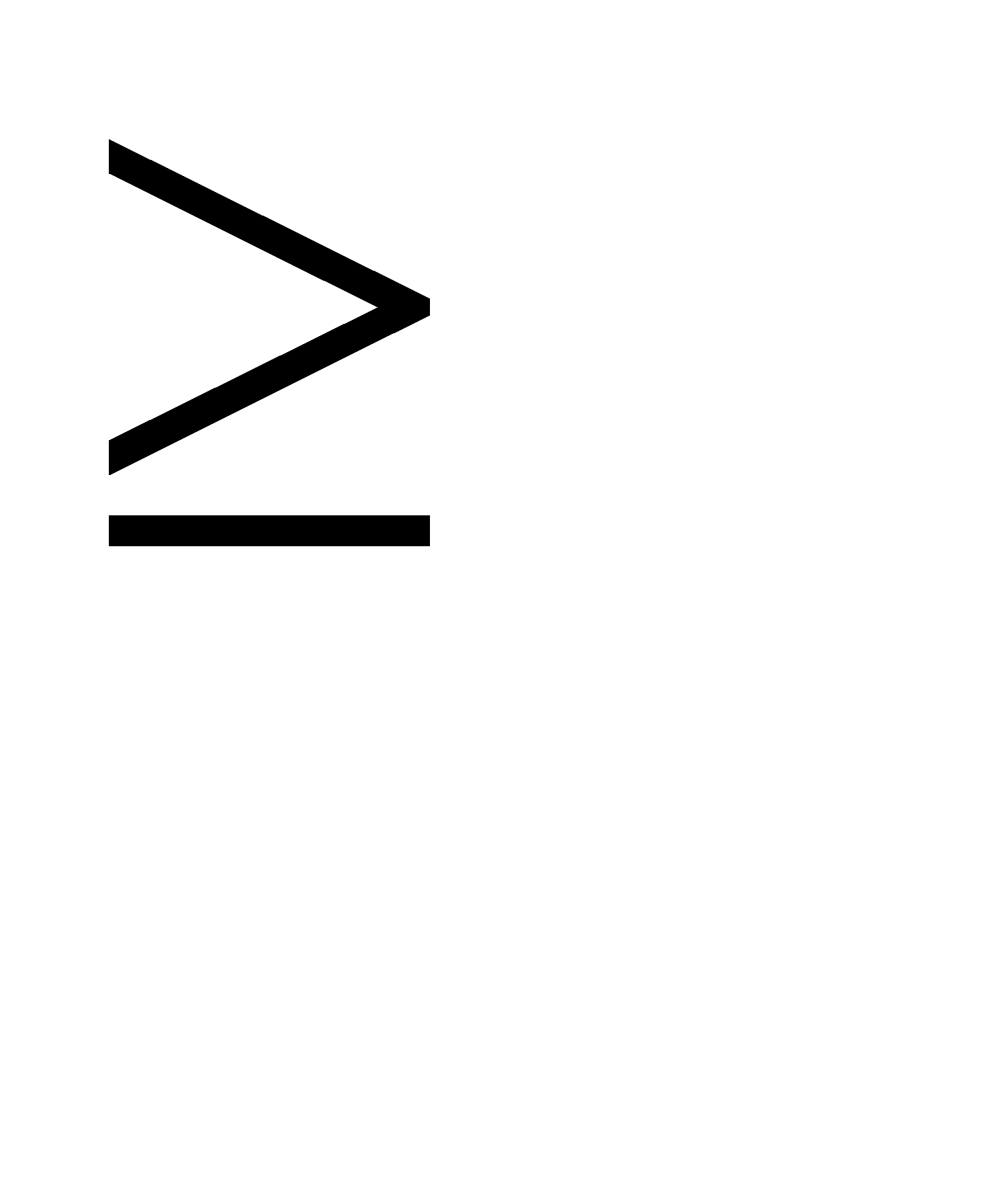 1 интегральное уравнение не имеет характеристических чисел, а значит, и собственных функций.
1 интегральное уравнение не имеет характеристических чисел, а значит, и собственных функций.
3) 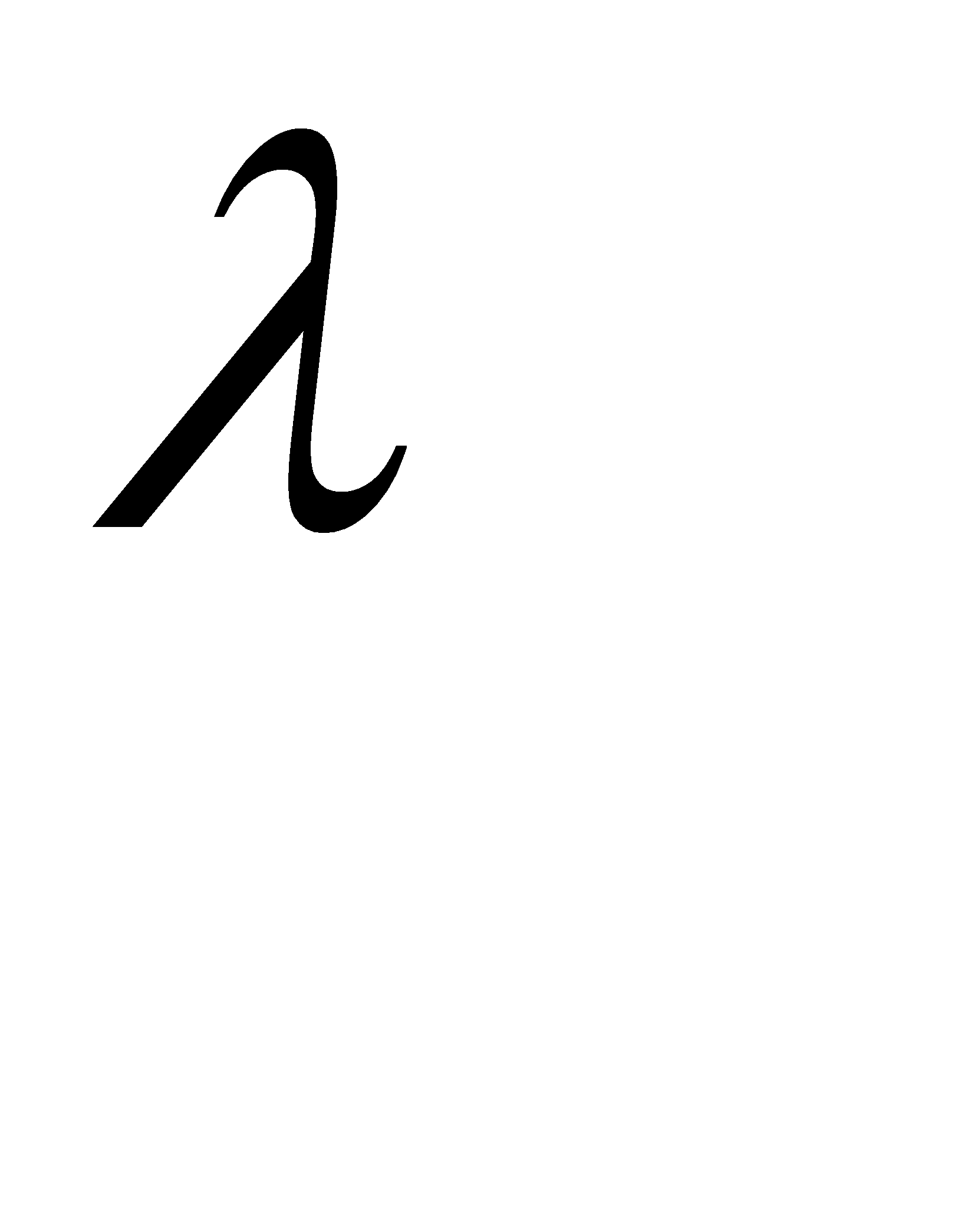 - 1<0 или
- 1<0 или 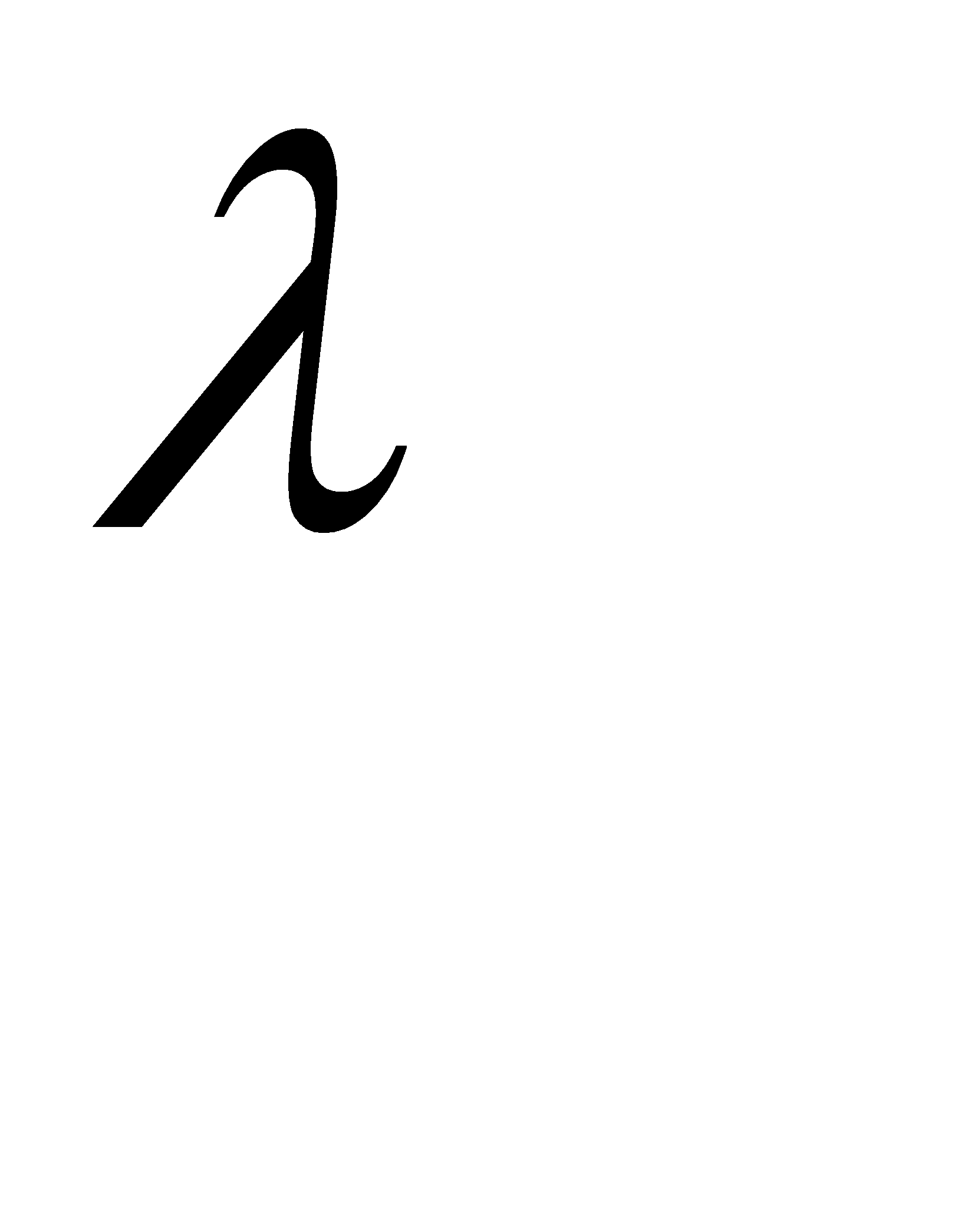 < 1. Общее решение уравнения (3) будет
< 1. Общее решение уравнения (3) будет
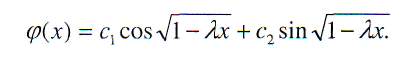
Отсюда находим, что 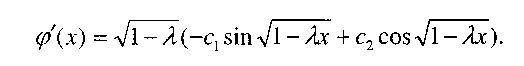
Краевые условия (4) в этом случае дают для нахождения с, и с2 систему
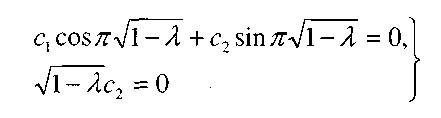 (5)
(5)
Определитель этой системы
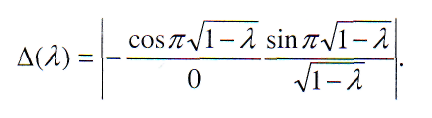
Полагая его равным нулю, получим уравнение для нахождения характеристических чисел:
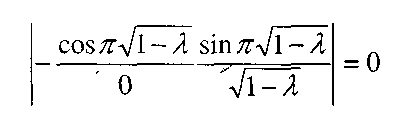 (6)
(6)
или 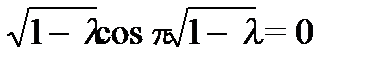 . По предположению
. По предположению 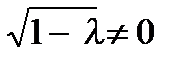 поэтому
поэтому 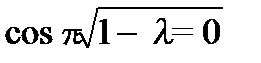 . Отсюда находим, что
. Отсюда находим, что 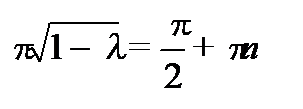 , где
, где 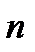 -любое целое число.
-любое целое число.
Все корни уравнения (6) даются формулой
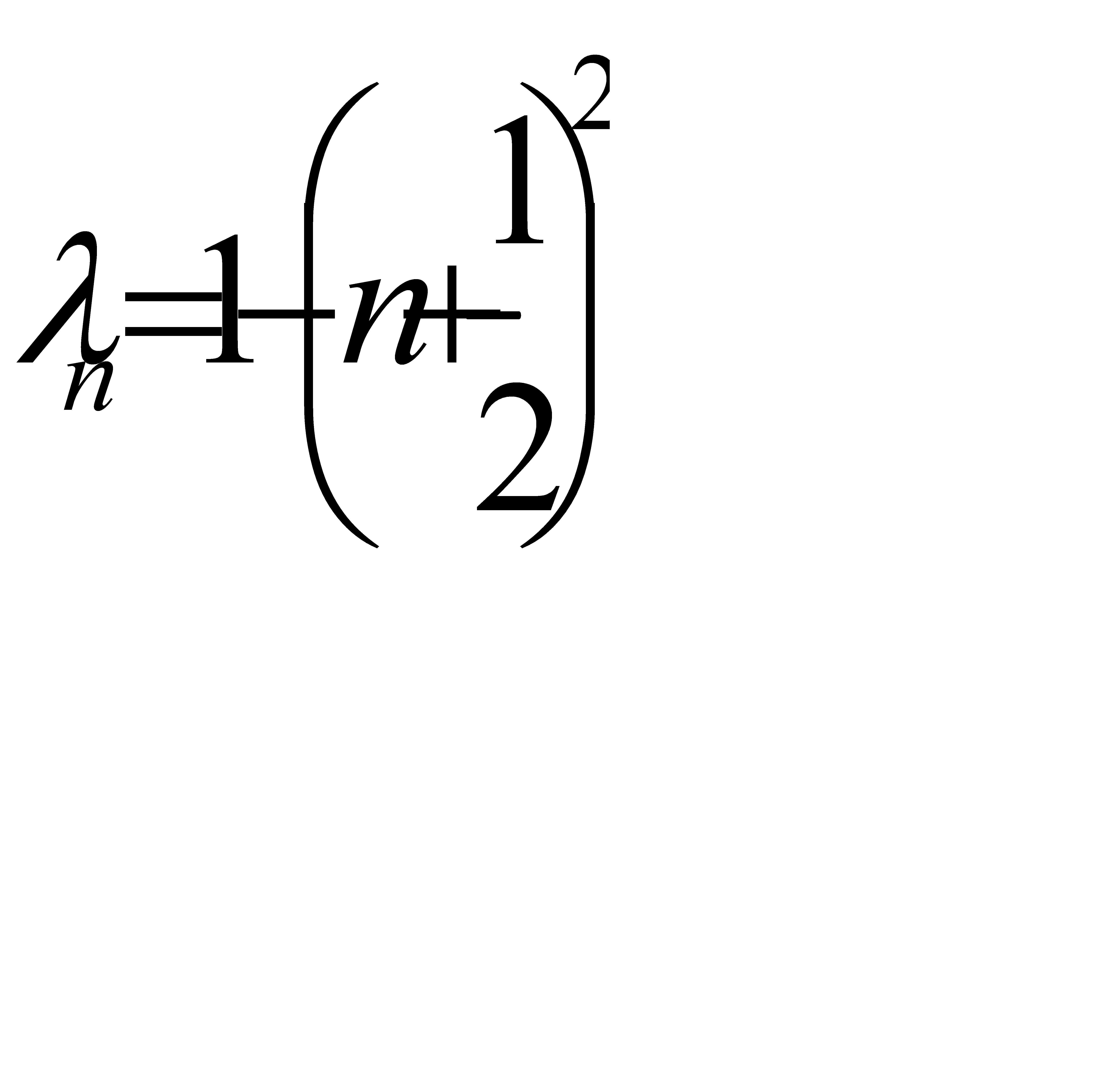
При значениях 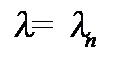 система принимает вид
система принимает вид
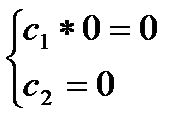
Она имеет бесконечное множество ненулевых решений
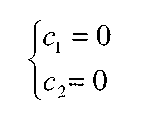
где с - произвольная константа. Значит, и исходное интегральное уравнение имеет бесконечное множество решений вида
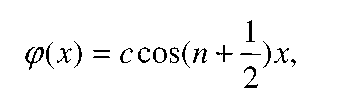
которые являются собственными функциями этого уравнения.
Итак, характеристические числа и собственные функции данного интегрального уравнения будут,
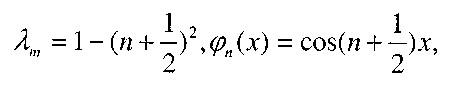
где п- любое целое число.
 2015-03-08
2015-03-08 8458
8458








