.Сведение дифференциальных уравнений к интегральным.
В ряде случаев решение того или иного дифференциального уравнения целесообразно сводить к решению интегрального уравнения.
Например, для доказательства существования и единственности решения дифференциального уравнения
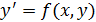
с начальным условием 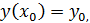 удобно свести его к интегральному уравнению (нелинейному)
удобно свести его к интегральному уравнению (нелинейному)
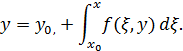
Сведение к интегральному уравнению возможно и для дифференциальных уравнений выше первого порядка.
Рассмотрим, например, уравнение второго порядка
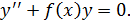
Положив 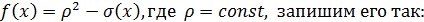

Как известно, решение уравнения
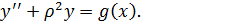
Можно представить в виде
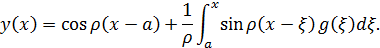
Поэтому, нахождение решения уравнения (1.9) сводится к решению интегрального уравнения
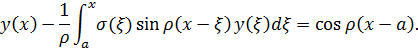
-------------------------------------------------------------------------------------------------
. Сведение дифференциальных уравнений к интегральным.
В ряде случаев решение того или иного дифференциального уравнения целесообразно сводить к решению интегрального уравнения. Например, для доказательства существования и единственности решения дифференциального уравнения
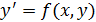
с начальным условием 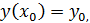 удобно свести его к интегральному уравнению (нелинейному)
удобно свести его к интегральному уравнению (нелинейному)
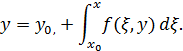
Сведение к интегральному уравнению возможно и для дифференциальных уравнений выше первого порядка.
Рассмотрим, например, уравнение второго порядка
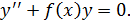
Положив 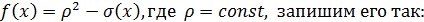

Как известно, решение уравнения
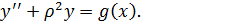
Можно представить в виде
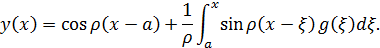
Поэтому, нахождение решения уравнения (1.9) сводится к решению интегрального уравнения
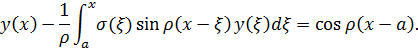
Рассмотрим пример решения уравнения Вольтерра методом дифференцирования.
y(x) + 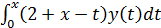 =
= 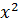
Решение
Дифференцируя дважды по x, получаем:
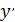 (x) + 2y(x)+
(x) + 2y(x)+ 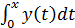 = 2x
= 2x
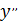 (x) + 2
(x) + 2 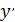 (x) + y(x) = 2 ……(1)
(x) + y(x) = 2 ……(1)
При x=0: y(0) =0 и 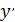 (0)=0…….(2)
(0)=0…….(2)
Характеристическое уравнение для дифференциального уравнения 2-го порядка имеет вид: 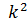 + 2k + 1 = 0
+ 2k + 1 = 0
Его корни 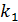 =
= 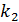 = - 1
= - 1
Общее решение для соответствующего однородного уравнения имеет вид:
Y(x) = 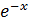 (
(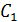 +
+ 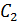 x)
x)
Найдем частное решение неоднородного уравнения по виду правой части:
Ф (х) = А, где А=2
Общее решение неоднородного уравнения:
y(x) = Y(x) + ф(x)
y(x) = 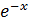 (
(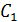 +
+ 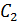 x) +2 …..(3)
x) +2 …..(3)
Найдем производную 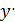 (x) = -
(x) = - 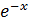 (
(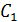 +
+ 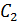 x) +
x) + 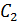
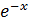
Из условий (2) найдем при x=0:
y(0) = 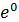 (
(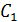 +
+ 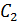 0) +2 = 0,
0) +2 = 0, 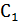 = -2
= -2
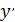 (0) = -
(0) = - 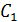 +
+ 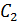 = 0,
= 0, 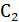 = -2
= -2
Окончательно, y(x) = -2 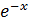 (1+x) +2
(1+x) +2
2/.Решить уравнение
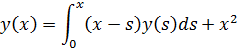
Продифференцируем уравнение дважды:
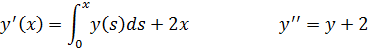
Решая получившиеся дифференциальное уравнение, с учетом условий
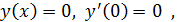 находим
находим 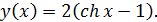
Задание для самостоятельной работы:
Методом дифференцирования решить следующие интегральные уравнения
1) 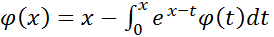
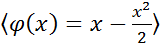
2) 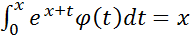
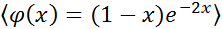
3) 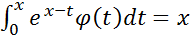
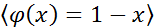
4) 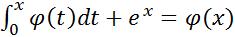
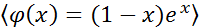
 2015-03-08
2015-03-08 3644
3644








