2015-03-08
386
Во многих случаях удается избежать противоречий наивной теории множеств, если выбрать некоторое так называемое универсальное множество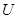 
и ограничиться рассмотрением только его подмножеств.
Если некоторые множества взять в качестве исходных, то из них можно получить новые с помощью следующих операций.
Объединением множеств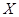 
и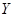 
(обозначение 
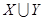) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств 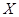или :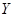
.
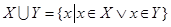Вместо символа объединения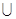 
используется также символ +.
Пересечением множеств 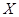и 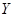(обозначение 
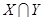) называется множество, состоящее из элементов, принадлежащих каждому из множеств 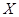и :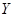
.
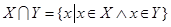Для операции пересечения используются также другие обозначения:
.
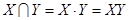Аналогично определяются объединение и пересечение произвольной совокупности множеств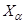 
, 
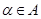. Здесь 
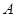– множество индексов. Если 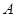– множество 
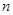первых натуральных чисел, то употребляются обозначения 
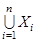и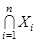 
, а в случае если 
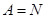, то будем писать 
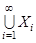и 
.
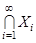Разностью множеств 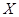и 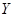(обозначение 
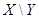) называется множество, состоящее из всех элементов 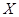, не принадлежащих :
.
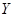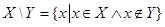В отличие от двух предыдущих операций разность некоммутативна: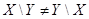 
. Если 
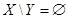, то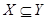 
.
Симметрической разностью множеств 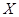и 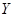(обозначение 
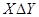) называется множество элементов 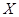и 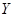, которые содержатся только в одном из этих множеств:
.
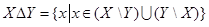Дополнением к множеству 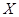(обозначение 
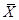) относительно универсального множества 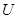называется множество:
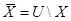или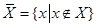 
.
Операции объединения, пересечения и дополнения часто называют булевыми операциями над множествами. Так как операция разности не обладает свойством ассоциативности, то ее выражают через другие операции, например, операции дополнения и пересечения:
.
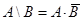Универсальное множество позволяет геометрически изображать множества и операции над ними с помощью диаграмм Венна (рис. 1).
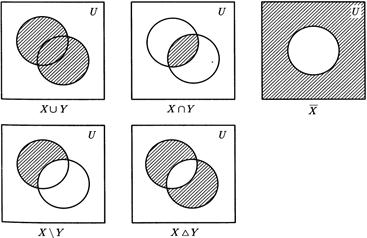
Рис. 1. Диаграммы Венна
