каждому кратному корню кратности k соответствует k -1 простейшая второго вида с убывающими степенями знаменателя и одна простейшая первого вида,
каждым двум некратным комплексным корням соответствует простейшая третьего вида.
Пример 9. Разложить на простейшие рациональную дробь 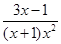 .
.
Решение. Корни знаменателя: х 1 = -1 действительный некратный корень, и х 2 = 0 действительный кратный корень кратности 2. Следовательно
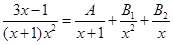 .
.
Для того, чтобы найти неизвестные коэффициенты А, В1 и В2 приведем правую часть выражения к общему знаменателю, раскроем скобки и приведем подобные члены в числителе
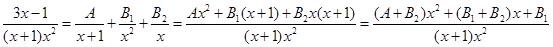
Приравняем числители исходного и конечного выражений
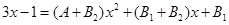 .
.
Такое соотношение возможно тогда и только тогда когда совпадают коэффициенты при одинаковых степенях х (если какая-то степень х отсутствует, то это значит, что коэффициент при ней равен нулю). Получим систему
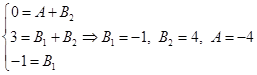
Окончательно
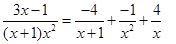
Пример 10. Разложить на простейшие рациональную дробь 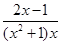 .
.
Решение. Корни знаменателя: х 1=0 действительный некратный корень, и два комплексных корня квадратного трехчлена 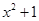 с отрицательным дискриминантом
с отрицательным дискриминантом
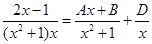 .
.
Для того, чтобы найти неизвестные коэффициенты А, В и D приведем правую часть выражения к общему знаменателю, раскроем скобки и приведем подобные члены
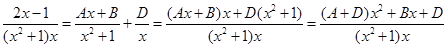
Приравняем числители и коэффициенты при одинаковых степенях х
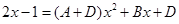 .
.
Получим систему
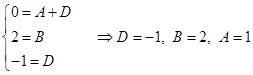
Окончательно
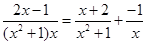 .
.
Вычислим интегралы от рациональных дробей примеров 9 и 10, используя формулы (1.15-1.19).
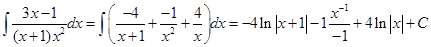
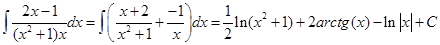
Замечание. Существует большое количество интегралов, которые методом замены переменной можно свести к интегралам от рациональных дробей. К таким интегралам относятся интегралы от иррациональных функций вида
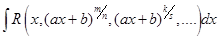
В этом случае надо сделать замену переменной вида 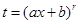 , где r – общий знаенатель дробей m/n, k/s…
, где r – общий знаенатель дробей m/n, k/s…
Пример. Вычислить интеграл 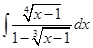 .
.
Решение. Степени корней ¼ и 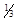 имеют общий знаменатель 12. Следовательно, замена
имеют общий знаменатель 12. Следовательно, замена
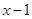 =
= 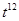
 2015-03-07
2015-03-07 443
443








