Глава 1. Площадь криволинейной трапеции

Пусть на отрезке [a,b] задана неотрицательная непрерывная функция f(x). На плоскости XOY, как показано на рис.1.1, график этой функции, отрезок оси абсцисс и прямые x = a и y = b образуют криволинейную трапецию, площадь такой криволинейной трапеции равна S.

Разделим отрезок [ a, b ] на произвольные n частей, при этом координаты точек деления удовлетворяют соотношению

x ₀= a < x ₁< x ₂<... < x _{i -1}< x _i<... < x _n = b.

В точках деления проведем прямые, перпендикулярные оси ОХ. Криволинейная трапеция разделилась на n узких криволинейных трапеций (элементарных трапеций) шириной Δ x _i = x _i - x _i_-1(i = 1, 2…n). Площадь каждой такой элементарной трапеции обозначим как Δ S _i.

На каждом промежутке [ x _i_-1, x _i] выберем произвольную точку 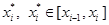, вычислим в точке 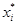функцию 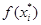. Каждую i -ю полоску заменим на соответствующий прямоугольник, высота которого равна 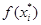. Тогда площадь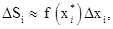

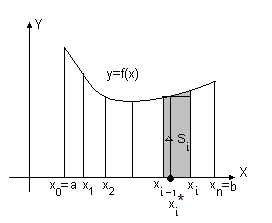
Рис. 1.1. Криволинейная трапеция.

Сумма площадей полученных прямоугольников приближенно равна площади исходной криволинейной трапеции.

S» . (1.1)

Увеличим число разбиений n. При этом каждый раз обязательно должна уменьшатся длина наибольшего из разбиений Δ x _i. Эту длину называют рангом дробления и обозначают r, т.е. r = max Δ x _i ® 0 при n ® ¥. При этом погрешность при вычислении площади будет стремиться к нулю и в пределе мы получим площадь криволинейной трапеции, т.е.

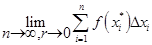= S (1.2)