1. если p 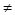 1,
1, 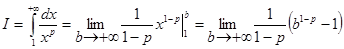 ,
,
2. если p = 1, 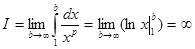 ,
,
Вывод: сходимость интеграла I зависит от значения параметра р:
если р > 1, то 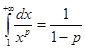 , т.е. интеграл сходится,
, т.е. интеграл сходится,
если р < 1, то 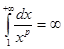 , т.е. интеграл расходится,
, т.е. интеграл расходится,
если р = 1, то 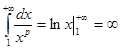 интеграл расходится.
интеграл расходится.
Несобственные интегралы от разрывных функций. Пусть функция f(x) определена и непрерывна на [a,b] за исключением точки с Î [a,b]. Рассмотрим три случая.
1. Функция терпит разрыв в точке b. Интеграл от функции f (x) с точкой разрыва на верхнем пределе определяется так
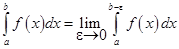
Пример. Вычислить интеграл 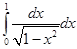 .
.
Решение.
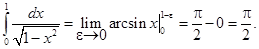
2. Функция терпит разрыв в точке а. Тогда по аналогии с предыдущим случаем интеграл с точкой разрыва на нижнем пределе определяется так
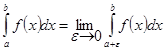
Пример. Исследовать интеграл 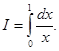 Здесь подынтегральная функция
Здесь подынтегральная функция 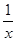 не существует в точке х = 0, поэтому
не существует в точке х = 0, поэтому
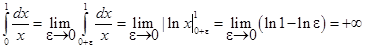
Таким образом, данный интеграл расходится (не существует).
3. Функция имеет разрыв во внутренней точке отрезка [a,b], т.е. a < c < b.
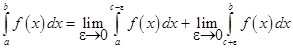
Пример. Вычислить интеграл 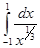 .
.
Решение. Подынтегральная функция терпит разрыв в точке 0. Поэтому
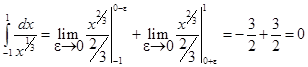
 2015-03-07
2015-03-07 360
360








