Теорема. Первообразная как интеграл с переменным верхним пределом. Если функция f (x) непрерывна на интервале [a,b], то функция Ф(х) = 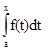 , где
, где 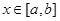 , дифференцируема в любой внутренней точке х этого интервала, причем Ф¢(x) = f (x), то есть функция Ф(х) является первообразной функции f(x). Функция Ф(х) называется интегралом с переменным верхним пределом.
, дифференцируема в любой внутренней точке х этого интервала, причем Ф¢(x) = f (x), то есть функция Ф(х) является первообразной функции f(x). Функция Ф(х) называется интегралом с переменным верхним пределом.
Доказательство. Найдем производную функции Ф(x). Для этого вначале выберем приращение аргумента D х столь малым, чтобы точка х + D х лежала внутри отрезка [a,b], и найдем приращение функции Ф(х) (рис. 3.1), приращение обозначено зеленым цветом).
DФ(х) = Ф(х + D х) - Ф(х) = 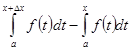 =
= 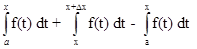
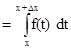
Здесь мы использовали свойство аддитивности. К полученному интегралу применим теорему о среднем
DФ(x) = 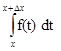 = f(с)Dx, где с Î [ x, x +D x ].
= f(с)Dx, где с Î [ x, x +D x ].
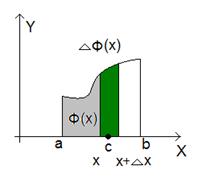
Рис. 3.1. Интеграл с переменным верхним пределом.
Следовательно, 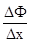 = f (с). Поскольку f (x) непрерывна и с ® x, если D х ® 0, то
= f (с). Поскольку f (x) непрерывна и с ® x, если D х ® 0, то 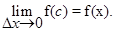 Поэтому производная функции Ф(х) равна f(x)
Поэтому производная функции Ф(х) равна f(x)
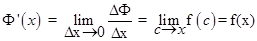 . (3.1)
. (3.1)
А так как производная функции Ф(х) равна f(x), то, по определению первообразной, Ф(х) первообразная. Следовательно, интеграл от функции f (x) с постоянным нижним и переменным верхним пределом х, есть одна из первообразных функции f (x) 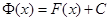 .
.
Этот факт показывает, что дифференциальное и интегральное исчисление представляет собой нечто единое и известен, как основная теорема математического анализа.
Теорема. Формула Ньютона – Лейбница.
Если функция f(x) непрерывна на интервале [a,b], то определенный интеграл равен разности значений первообразной 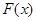 на концах промежутка
на концах промежутка
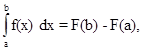 (3.2)
(3.2)
Доказательство. В силу непрерывности на отрезке [a,b] функция f(x) интегрируема и, на основании предыдущей теоремы, имеет первообразную
Ф(x) = 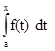 = F(x) + C. (3.3)
= F(x) + C. (3.3)
Константу С легко выразить через значение первообразной F(х) в точке а. Действительно принимая во внимание, что
Ф(а) = 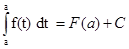 = 0 (3.4)
= 0 (3.4)
из (3.4) получим:
- F (a) = C. (3.5)
Поскольку
Ф(b) = 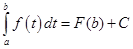 , (3.6)
, (3.6)
то, подставив (3.5) и (3.6) в (3.3) получим основную формул математического анализа - формулу Ньютона – Лейбница
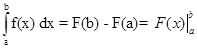 (3.7)
(3.7)
где F (x) - первообразная для функции f (x), а 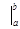 - знак подстановки Ньютона. Этот знак означает, что сперва в функцию F (x) подставляем верхний предел и вычитаем функцию вычисленную в точке нижнего предела.
- знак подстановки Ньютона. Этот знак означает, что сперва в функцию F (x) подставляем верхний предел и вычитаем функцию вычисленную в точке нижнего предела.
Формула (3.5) дает следующее правило: для вычисления определенного интеграла необходимо найти первообразную подынтегральной функции, т.е. вычислить неопределенный интеграл, а затем вычислить разность значений первообразной на верхнем и нижнем пределе.
Пример 1. Вычислить интеграл 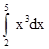 .
.
Решение. 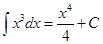 . Следовательно, по формуле (3.7)
. Следовательно, по формуле (3.7)
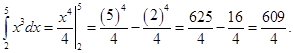
При вычислении определенного интеграла используются те же основные приемы, что и при вычислении неопределенного интеграла.
 2015-03-07
2015-03-07 636
636








