2015-03-08
549
1) Даны точки A и B своими координатами. Известно, что точка C делит отрезок AB в отношении l. Найти длину отрезка AB и координаты точки C. На координатной плоскости отметить точки A, B и С:
а) A (-2; 3), B (4; 2), l =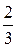 
;
б) A (3; -2), B (-4; 2), l =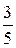 
;
в) A (2; -4), B (4; -2), l =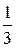 
.
Решение. а) По теореме 1.2.2 имеем
| АВ |=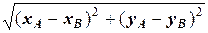 
= 
= 
.
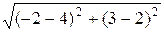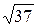По той же теореме
xC =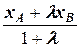 
= 
= 
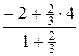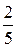, yC = 
= 
= 
,
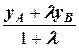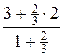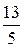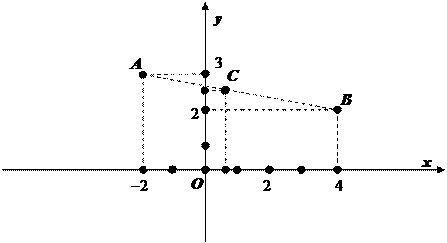
то есть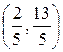 
- координаты точки С.
На координатной плоскости отметим точки A, B и С:
Ответ: Длина отрезка АВ равна 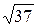, координаты точки C равны .
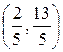2) Даны вершины треугольника АВС. Найти длины сторон треугольника и координаты точки пересечения медиан. Сделать чертёж:
а) A (-2; 3), B (3; 1), С (-5; -4);
б) A (3; -2), B (-4; 2), С (4; -3);
в) A (2; -4), B (4; -2), С (-2; 3).
Решение. а) По теореме 1.2.2 имеем
| АВ |= =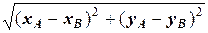 
= 
,
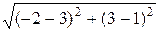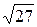| АС |=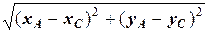 
= 
= 
,
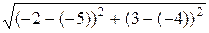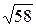| BС |=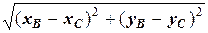 
= 
= 
.
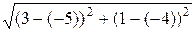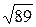Медианы треугольника пересекаются в одной точке D и делятся в отношении l =2, если считать от вершины треугольника (то есть если медиана опущена из вершины C к середине K противолежащей стороны AB, то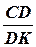 
=2). Найдём координаты точки K:
xK =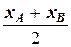 
= 
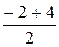=1, yK = 
= 
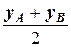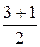=2,
то есть (1; 2) - координаты точки K.
Теперь можем найти координаты точки пересечения медиан:
|
|
|
xD =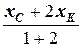 
= 
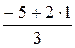= -1, yD = 
= 
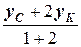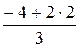=0,
то есть (-1; 0) - координаты точки D.
Ответ: а) Длины сторон треугольника: | АВ |= 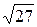, | АС |= 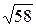, | BС |= 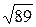. D (-1; 0) - точка пересечения медиан.
