 2.1.1. Возьмём положительное направление оси Ox вместе с началом координат. Тогда положение любой точки A, отличной от O, однозначно определяется парой (r, j), где r - расстояние от точки O до точки A (r =| OA |), j - угол между положительным направлением Ox и лучом OA, - p < j £ p (угол измеряется, как правило, в радианах, но это не совсем обязательно) (рис. 2.1).
2.1.1. Возьмём положительное направление оси Ox вместе с началом координат. Тогда положение любой точки A, отличной от O, однозначно определяется парой (r, j), где r - расстояние от точки O до точки A (r =| OA |), j - угол между положительным направлением Ox и лучом OA, - p < j £ p (угол измеряется, как правило, в радианах, но это не совсем обязательно) (рис. 2.1).
При этом предполагается, что измерение угла, как обычно, производится так, что j >0, если измерение производится против часовой стрелки, и j <0, если измерение производится по часовой стрелки.
Пара (r, j) называется полярными координатами точки A, r - полярный радиус, j - полярный угол, O - полярный полюс, а луч Ox - полярная ось.
Как и в прямоугольной декартовой системе координат, запись A (r, j) означает, что точка A имеет полярные координаты (r, j).
2.1.2. При изображении положения точки A относительно полярной системы координат ось Oy не изображается, а у оси Ox изображается только положительная полуось без стрелки. Для того, чтобы построить точку A (r, j) достаточно провести луч OK под углом j от луча Ox и отложить точку A на расстоянии r от точки O.
 Пример 1. Построить точку A
Пример 1. Построить точку A 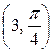 .
.
Решение. Проведём луч OK под углом j = 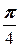 от луча Ox и отложим точку A на расстоянии r =3 от точки O.
от луча Ox и отложим точку A на расстоянии r =3 от точки O.
2.1.3. Существует очевидная связь между прямоугольной декартовой и полярной системами координат:
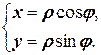 (2.1.1)
(2.1.1)
 Эта связь легко усматривается из простых геометрических соображений. Действительно, если точка A задана своими полярными и прямоугольными координатами - A (r, j) и А (xA, yA), то xA = r cos j, yA = r sin j (рис. 2.2).
Эта связь легко усматривается из простых геометрических соображений. Действительно, если точка A задана своими полярными и прямоугольными координатами - A (r, j) и А (xA, yA), то xA = r cos j, yA = r sin j (рис. 2.2).
Эту связь можно выразить иначе:
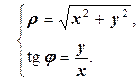 (2.1.2)
(2.1.2)
Примеры. 2) Дана точка A 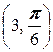 своими полярными координатами. Найдём её прямоугольные координаты. По формулам (2.1.1) имеем xA =3cos
своими полярными координатами. Найдём её прямоугольные координаты. По формулам (2.1.1) имеем xA =3cos 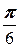 =3×
=3× 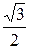 =
= 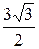 , yA =3sin
, yA =3sin 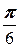 =3×
=3× 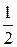 =
= 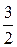 , то есть
, то есть 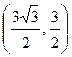 - прямоугольные координаты точки A.
- прямоугольные координаты точки A.
3) Дана точка A (4  , 4) своими прямоугольными координатами. Найдём её полярные координаты. По формулам (2.1.2) имеем
, 4) своими прямоугольными координатами. Найдём её полярные координаты. По формулам (2.1.2) имеем
r = 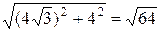 =8, tg j =
=8, tg j = 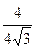 =
= 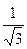 ,
,
откуда j = 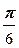 . Таким образом,
. Таким образом, 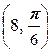 - полярные координаты точки A.
- полярные координаты точки A.
2.1.4. Упражнения. 1) Построить точки A 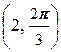 , B
, B 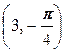 , C
, C 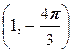 , D
, D 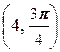 заданные своими полярными координатами.
заданные своими полярными координатами.
2) Найти прямоугольные координаты точек предыдущего задания.
3) Даны точки A ( , 1), B
, 1), B 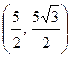 , C
, C 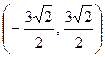 , D (-3
, D (-3  , 3) своими прямоугольными координатами. Найти её полярные координаты.
, 3) своими прямоугольными координатами. Найти её полярные координаты.
4) Найти расстояние между точками A и B, заданными своими полярными координатами:
а) A (3, 0), B 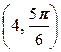 ;
;
б) A 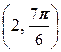 , B
, B 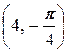 ;
;
в) A 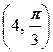 , B
, B 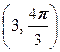 .
.
Решение. а) Найдём сначала прямоугольные координаты точек. Для точки A они совпадают с полярными: A (3, 0).
Для точки B: xB =4cos 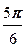 =4×
=4× 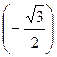 = -2
= -2  , yB =3sin
, yB =3sin 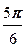 =4×
=4× 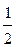 =2, то есть (-2
=2, то есть (-2  ; 2) - прямоугольные координаты точки B. Поэтому
; 2) - прямоугольные координаты точки B. Поэтому
| AB |= 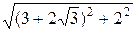 =
= 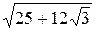 .
.
Ответ: | AB |= 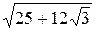 .
.
 2015-03-08
2015-03-08 1428
1428
