1) Точка A задана своими координатами в прямоугольной системе координат Oxy. Система Oxy подвергается параллельному переносу, O ¢ - начало новой системы O ¢ x ¢ y ¢. Найти координаты точки A в новой системе:
а) A (3, -4), O ¢ =(2, 1);
б) A (4, 2), O ¢ =(-2, 3);
в) A (2, -5), O ¢ =(3, -2).
Решение. а) Применяем формулу (3.1), из которой следует x ¢ = x - x 0, y ¢ = y - y 0, где (x 0, y 0) - координаты нового начала координат O ¢. Имеем x 0=2, y 0=1, x =3, y =-4. Поэтому x ¢ =3-2=1, y ¢ =-4-1=-5, то есть (1, -5) - координаты точки A в системе O ¢ x ¢ y ¢.
Ответ: (1, -5).
2) Известны: прямоугольные координаты точки A в новой системе, которая получена параллельным переносом; координаты начала O ¢ в старой системе. Найти координаты A в старой системе:
а) A (3, -4), O ¢ =(2, 1);
б) A (4, 2), O ¢ =(-2, 3);
в) A (2, -5), O ¢ =(3, -2).
Решение. Указание. Известны (x 0, y 0) и (x ¢, y ¢) из формул (3.1). Найти (x, y).
3) Новая прямоугольная система Ox ¢ y ¢ получается поворотом вокруг начала О на угол a. Известны новые координаты точки А. Найти старые:
а) a = 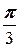 , A (4, -2);
, A (4, -2);
б) a = 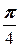 , A (-3, 1);
, A (-3, 1);
в) a = 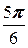 , A (2, 3).
, A (2, 3).
Решение. а) Применяем формулы (3.3). Имеем a = 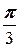 , (x ¢, y ¢) =(4, -2). Поэтому
, (x ¢, y ¢) =(4, -2). Поэтому
x =4cos 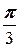 -(-2)sin
-(-2)sin 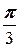 =4×
=4× 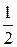 +2×
+2× 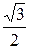 =2+
=2+  ,
,
y =4sin 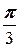 +(-2)cos
+(-2)cos 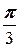 =4×
=4× 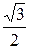 -2×
-2× 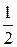 =2
=2  -1,
-1,
то есть (2+  , 2
, 2  -1) - старые координаты точки А.
-1) - старые координаты точки А.
Ответ: а) (2+  , 2
, 2  -1).
-1).
4) Новая прямоугольная система Ox ¢ y ¢ получается поворотом вокруг начала О на угол a. Известны старые координаты точки А. Найти новые:
а) a = 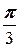 , A (4, -2);
, A (4, -2);
б) a = 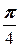 , A (-3, 1);
, A (-3, 1);
в) a = 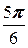 , A (2, 3).
, A (2, 3).
Решение. а) В формуле (3.3) имеем a = 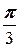 , (x, y) =(4, -2), то есть имеем систему
, (x, y) =(4, -2), то есть имеем систему
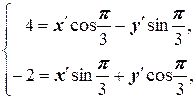 Û
Û 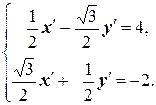
Решаем последнюю систему:
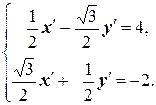 Û
Û 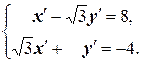
Далее воспользуемся правилом Крамера:
D= 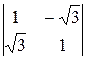 =4, D1=
=4, D1= 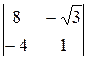 =8-4
=8-4  , D2=
, D2= 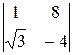 =-4-8
=-4-8  ,
,
x ¢ = 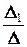 =
= 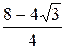 =2-
=2-  , y ¢ =
, y ¢ = 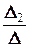 =
= 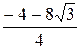 =-1-2
=-1-2  ,
,
то есть (2-  , -1-2
, -1-2  ) - новые координаты точки А.
) - новые координаты точки А.
Ответ: а) (2-  , -1-2
, -1-2  ).
).
 2015-03-08
2015-03-08 572
572








