Прямоугольная пластинка (рис. К3.0-К3.5) или круглая пластина радиуса R=60 см (рис. К3.6-К3.9) вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в табл. К3 (при знаке минус направление ω противоположного показанному на рисунке). Ось вращения на рис.0-3 и 8,9 перпендикулярна плоскости пластины и проходит через точку O (пластина вращается в своей плоскости); на рис. 4-7 ось вращения OO1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис.0-5) или по окружности радиуса R, т.е. по ободу пластины (рис. 6-9), движется точка М. Закон её относительного движения, выражаемый уравнением s=AM=f(t) (s – в сантиметрах, t – в секундах), задан в табл.К3, при этом на рис. 6-9 s=AM и отсчитывается по дуге окружности; там же даны размеры b и ℓ. На всех рисунках точка М показана в положении, при котором s=AM>0 (при s<0 точка М находится по другую сторону от точки А.)
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1=1c.
Указания. Задача К3 – на сложное движение точки. При её решении движение точки по пластине считать относительным, а вращательное движение самой пластины – переносным и воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить расчёты, следует изобразить точку М на пластине в том положении, в котором нужно определить её абсолютную скорость (или ускорение), а не в произвольном положении, показанном на рисунках к задаче.
Таблица К3
| Номер условия | 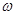 , 1/c , 1/c | Рис. 0-5 | Рис. 6-9 | ||
| b, см | s=AM | ℓ | S=AM=f(t) | ||
| -2 | 60(t4-3t2)+56 | R | 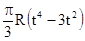 | ||
| 60(t3-2t2) | R | 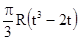 | |||
| 80(2t2-t3)-48 | R | 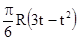 | |||
| -4 | 40(t2-3t)+32 | 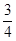 R R | 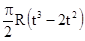 | ||
| -3 | 50(t3-t)-30 | R | 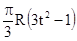 | ||
| 50(3t-t2)-64 | R | 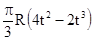 | |||
| 40(t-2t3)-40 | 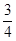 R R | 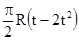 | |||
| -5 | 80(t2-t)+40 | R | 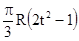 | ||
| 60(t-t3)+24 | R | 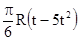 | |||
| -5 | 40(3t2-t4)-32 | 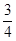 R R | 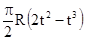 |
| |||
|
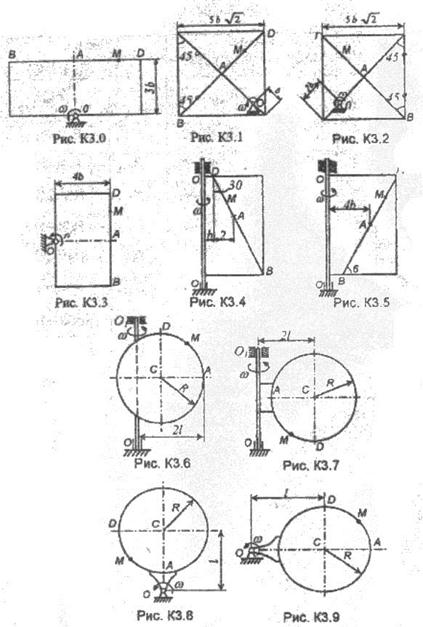
Пример К3. Треугольная пластина АDE вращается вокруг оси z по закону j = f1(t) положительное направление отсчета угла j показано па рисунке дуговой стрелкой. По гипотенузе АD движется точка В по закону s = AB = f2(t); положительное направление отсчета s – от А к D.
Дано: j = 0,1t3 – 2,2t, s = AB = 2+15t – 3t2; (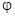 - в радианах, s – в сантиметрах, t – в секундах).
- в радианах, s – в сантиметрах, t – в секундах).
Определить: 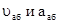 в момент времени t1=2c.
в момент времени t1=2c.
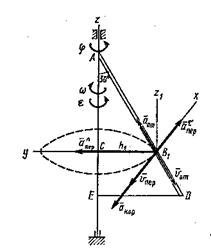
Решение. Рассмотрим движение точки В как сложное, считая ее движение по прямой АD относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость 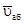 и абсолютное ускорение
и абсолютное ускорение 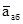 точки найдутся по формулам:
точки найдутся по формулам:
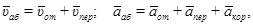
где, в свою очередь,
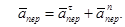
Определим все характеристики относительного и переносного движений.
1. Относительное движение. Это движение прямолинейное и происходит по закону
s = AB = 2+15t – 3t2
Поэтому 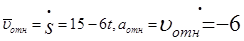
В момент времени t1=2 c имеем
S1 = AB1 = 20 cм, v отн = 3 cм/с, 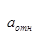 = -6 cм/с2.
= -6 cм/с2.
Знаки показывают, что вектор v отн направлен в сторону положительного отсчета расстояния s, а вектор 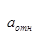 - в противоположную сторону. Изображаем векторы на рисунке.
- в противоположную сторону. Изображаем векторы на рисунке.
2. Переносное движение. Это движение (вращение) происходит по закону j = 0,1t3 – 2,2t. Найдем угловую скорость 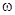 и угловое ускорение
и угловое ускорение 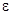 переносного вращения
переносного вращения 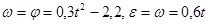 и при t1=2с,
и при t1=2с,
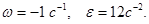
Знаки указывает, что в момент времени t1=2с направление e совпадает с направлением положительного отсчета угла 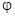 , направление
, направление 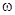 ему противоположно; отмети это на рисунке, соответствующими дуговыми стрелками.
ему противоположно; отмети это на рисунке, соответствующими дуговыми стрелками.
Из рисунка находим расстояние h1 точки В1 от оси вращения z: h1=AB1sin30° = 10 cм. Тогда в момент времени t1=2с, получим
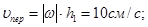
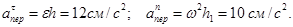
Изображаем на рисунке вектор 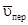 и
и 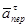 с учетом направления
с учетом направления 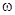 и вектор
и вектор 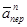 направлены векторы
направлены векторы 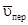 и
и 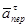 перпендикулярно плоскости ADE, а вектор
перпендикулярно плоскости ADE, а вектор 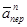 - по линии В1С к оси вращения.
- по линии В1С к оси вращения.
3. Кориолисово ускорение. Так как угол между вектором 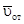 и осью вращения (вектором
и осью вращения (вектором 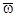 ) равен
) равен 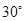 , то численно в момент времени t1=2 с
, то численно в момент времени t1=2 с
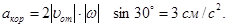
Направление 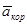 найдем,спроецировав вектор
найдем,спроецировав вектор 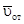 на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор
на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор 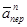 ), и повернув затем эту проекцию в сторону
), и повернув затем эту проекцию в сторону 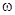 , т.е. по ходу часовой стрелки, на
, т.е. по ходу часовой стрелки, на 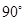 . Иначе направление
. Иначе направление 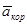 можно найти, учтя, что
можно найти, учтя, что 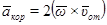 .Изображаем вектор
.Изображаем вектор 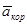 на рисунке.
на рисунке.
4. Определение 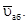 Так как
Так как 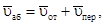 а векторы
а векторы 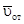 и
и 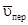 взаимно перпендикулярны (см. рис.), то в момент времени t1=2 с
взаимно перпендикулярны (см. рис.), то в момент времени t1=2 с
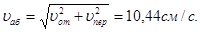
5. Определение 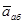 . По теореме о сложении ускорений
. По теореме о сложении ускорений
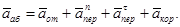
Для определения 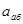 проведем координатные оси В1xyz1 и вычислим проекции вектора
проведем координатные оси В1xyz1 и вычислим проекции вектора 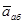 на эти оси. Учтем при этом, что векторы
на эти оси. Учтем при этом, что векторы 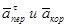 лежат на оси х, а векторы
лежат на оси х, а векторы 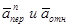 расположены в плоскости В1yz1, т.е. в плоскости пластины. Тогда, получим для момента времени t1=1 с:
расположены в плоскости В1yz1, т.е. в плоскости пластины. Тогда, получим для момента времени t1=1 с:
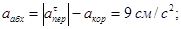
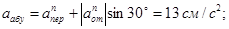
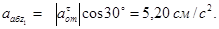
Отсюда находим значение 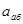 в момент времени t1=2 с:
в момент времени t1=2 с:
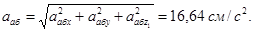
Ответ: 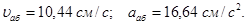
 2015-03-08
2015-03-08 3280
3280








