Определение положения центра тяжести тела.
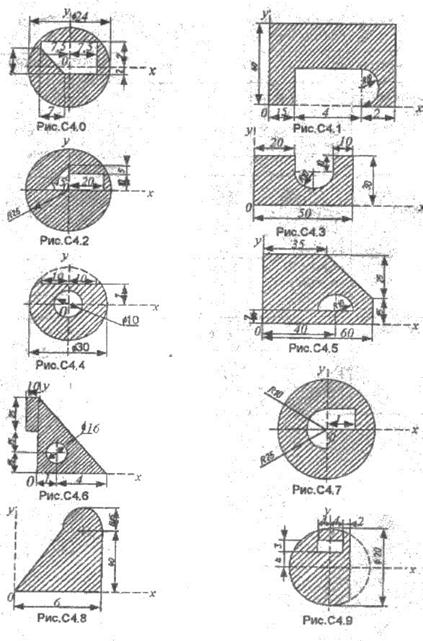
Найти координаты центра тяжести плоской фигуры, размеры указаны в сантиметрах, на рис. С4.0-С4.9
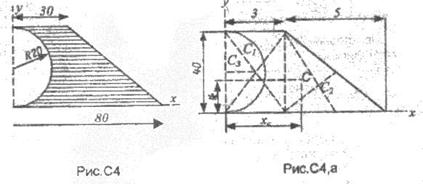
Пример выполнения задания. Определить координаты центра тяжести плоской фигуры, показанной на рис. С4.
Решение. Координаты центра тяжести плоской фигуры определяем по формулам:
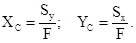
Здесь Sy=ΣFiXi, Sx=ΣFiYi – статические моменты фигуры относительно осей y и x, F – площадь фигуры.
Чтобы воспользоваться формулами (1), делим плоскую фигуру на части, для которых известны или легко определяются площади Fi и координаты центров тяжести Xi и Yi.
В данном случае, в качестве таких частей принимаем прямоугольник, треугольник и половину круга (рис. С4, а). Площадь половины круга, вырезанной из прямоугольника, считаем отрицательной.
Все данные расчёты заносим в таблицу (табл.1).
Таблица 1
| Номер элемента | 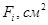 | 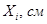 | 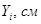 | 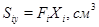 | 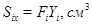 |
| 15,0 | 20,0 | ||||
| 46,7 | 13,3 | ||||
| -628 | 8,5 | 20,0 | -5338 | -12560 | |
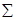 | - | - |
По формулам (1) вычисляем координаты центра тяжести плоской фигуры:
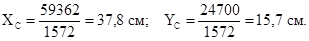
Центр тяжести площади указан на рис. С4, а.
Примечание. Площади и координаты центров тяжести некоторых плоских фигур, встречающихся при выполнении заданий, приведены в табл. 2.
Таблица 2
| Плоская фигура | Площадь | Координаты центра тяжести | |||
| Треугольник |
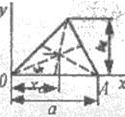 | 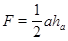 | 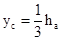 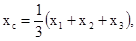 где где 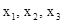 - координаты О, А, В - координаты О, А, В | ||
| Круговой сектор | 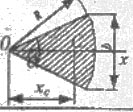 | 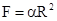 | 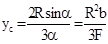 | ||
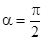 | 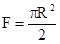 | 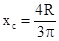 | |||
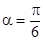 | 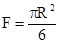 | 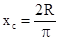 | |||
| Круговой сегмент | 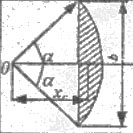 | 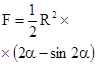 | 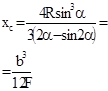 |
 2015-03-08
2015-03-08 1146
1146








