Нелинейные уравнения узловых напряжений

Как известно, стационарный режим электрической сети описывается следующей системой нелинейных алгебраических уравнений с комплексными переменными

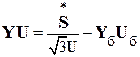, (1)

где 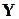– матрица узловых проводимостей, 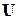– вектор неизвестных узловых напряжений, 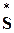– вектор узловых мощностей, 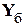– вектор проводимостей узлов по отношению к балансирующему, 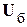– напряжение балансирующего узла.

В качестве исходной информации задается конфигурация сети и параметры схемы замещения, определяемые обычно указанием для каждой ветви номеров узлов начала и конца, сопротивления 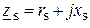и ёмкостной проводимости 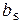для линий, сопротивления для трансформаторов. Параметры режима определяются узловыми мощностями 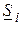и напряжением в балансирующем узле 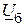. По параметрам сети определяется матрица узловых проводимостей. Обычно операции с комплексными переменными заменяются арифметическими операциями с действительными числами. При этом система комплексных уравнений, имеющая порядок n, определяемый по числу незави­симых узлов, преобразуется в систему из 2n уравнений с действительными пе­ременными.

Введем следующие обозначения:

,

.

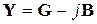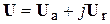При фиксированном значении узловых напряжений вектор задающих токов равен:

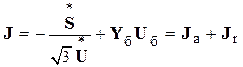(2)

Подставляя принятые обозначения в (1), получим:

.

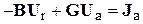
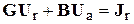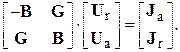(3)

Решение системы (3) позволяет найти составляющие 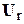и 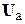вектора узловых напряжений.

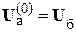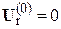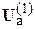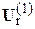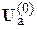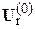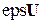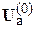Итерационный процесс поиска узловых напряжений начинается с задания исходного приближения, в качестве которого обычно принимают и . Затем определяются по (2) задающие токи и решается система (3). Найденные напряжения и сравниваются с исходными и . Если различие напряжений больше принятой точности расчёта по напряжению , то и 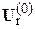заменяются на 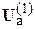и 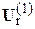, и расчет повторяется. При обеспечении заданной точности итерационный процесс заканчивается. Полученные напряжения в узлах используются для определения токов и потоков мощности в ветвях.

При этом сначала рассчитывается ток ветви:

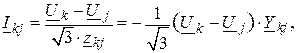
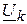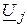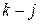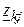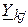где , – напряжения на концах ветви ; и – сопротив­ление и проводимость ветви.

Активные и реактивные составляющие тока можно найти следующим образом:

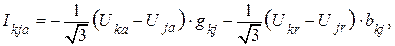
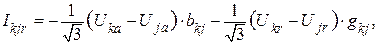
где 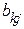, 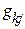– активная и реактивная составляющие проводимости линии между узлам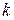и и .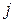

По токам в ветвях и напряжениям в узлах рассчитываются мощности:

в начале линии со стороны узла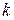

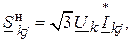
и в конце линии:

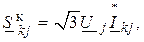
Активные и реактивные составляющие мощности определяют по следующим выражениям:

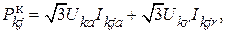
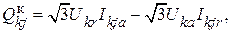
По найденным потокам мощности всех ветвей для каждого узла 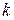, кроме балансирующего, определяется небаланс мощности:

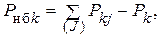
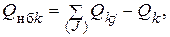
где 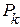, 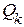– узловые мощности, 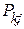, 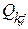– потоки по ветвям, связан­ным с узлом .

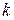Если небаланс в каждом узле не превышает допустимого значения, расчет заканчивается. В противном случае осуществляется возврат на продолжение итеративного процесса определения узловых напряжений при .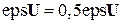

После обеспечения баланса в узлах определяются потери мощности по вет­вям и в целом по сети, а также другие параметры режима (модули напряжений, углы и т.п.).

Потери мощности можно найти по разности потоков мощности в начале и конце линии:

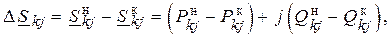
или по току ветви .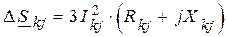

Если просуммировать эти значения по всем ветвям схемы, получим потери мощности для электрической сети.

Сумма потоков мощности для всех линий, связанных с балансирующим уз­лом, позволяет определить мощность, поступающую из балансирующего узла.

В комплексе программ (Regi, NetCAD, NetWORKS), разработанных на кафедре для анализа режимов, реализованы следующие методы решения системы (3) или (1): метод обращения матрицы проводимостей, метод Гаусса - Зейделя, градиентный метод, метод Ньютона первого порядка. Ниже приводится описание этих методов.