Метод Z-матрицы (метод обращения матрицы проводимостей)

При заданных или известных на очередной итерации напряжениях система нелинейных УУН:

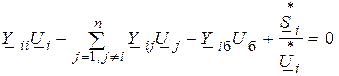
становится линейной следующего вида:

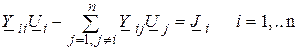
Эта же система в матричной записи:

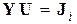, (4)

где компоненты вектора 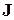определяются по формуле:

.

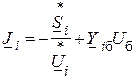Для неособенной (невырожденной) матрицы коэффициентов 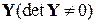, являющейся матрицей узловых и взаимных проводимостей узлов, существует обратная матрица 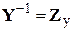, называемая матрицей собственных и взаимных сопротивлений узлов ( 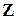–матрица). Умножая слева обе части системы (4) на 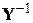, получим:

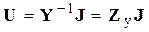
Полученные в результате решения СЛУ (4) напряжения 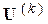следует считать исходными приближениями к искомым напряжениям 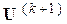. Поэтому применительно к нелинейной системе (1) итерационная процедура получения решения реализуется в виде:

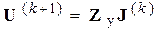(5)

Здесь токи 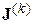в узлах уточняют на каждой итерации через напряжения предыдущей итерации 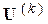по формуле (5). Далее по выражению (5) вычисляют новые приближения напряжений 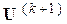. Такой процесс продолжается до выполнения критерия сходимости (если небаланс в каждом узле не превышает допустимого значения, расчет заканчивается).

Метод 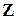– матрицы может оказаться эффективным в расчетах режимов ЭС с неизменным или мало изменяющимися конфигурацией и параметрами сети и при изменении нагрузок в узлах. В этом случае, обратив один раз матрицу 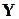, напряжения в узлах определяют через неизменную матрицу 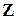и изменяющийся в соответствии с изменением нагрузок узлов вектор правых частей УУН.