Метод Гаусса – Зейделя

Систему линейных алгебраических уравнений (2) можно записать в виде

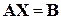
В матрице 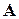, соответствующей узловым проводимостям, наибольшие элементы располагаются на главной диагонали, что обеспечивает необходимые условия сходимости итерационного процесса, основное соотношение которого:

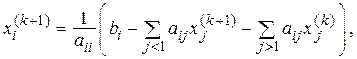
где 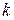– номер итерации.

Если хотя бы одна составляющая 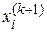вектора неизвестных отличается от значения 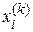на предыдущей итерации на величину, большую заданной точ­ности 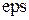, то итерационный процесс продолжается.

Метод достаточно простой в программной реализации и имеет неплохую сходимость. Ускорение итерационного процесса может быть достигнуто путем введения специальных ускоряющих коэффициентов 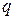, с помощью которых реализуемые значения неизвестных определяются по выражению

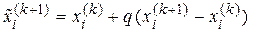
Величина 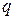выбирается в зависимости от хода итерационного процесса: при медленной апериодической сходимости принимают 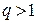, при колебательном характере процесса выбирается .

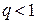Метод широко используется в промышленных программах анализа режи­мов сложных энергосистем. На кафедре реализован в программе NetWORKS.