Пусть 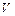 - область в трёхмерном пространстве. Векторным полем на
- область в трёхмерном пространстве. Векторным полем на 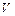 называется векторная функция
называется векторная функция 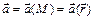 , заданная в точках
, заданная в точках 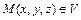 , где
, где 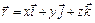 - радиус-вектор точки
- радиус-вектор точки 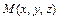 . Аналогично определяется плоское векторное поле.
. Аналогично определяется плоское векторное поле.
Векторной линией (силовой линией, линией тока) называется гладкая кривая, касательная к которой в каждой точке 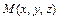 имеет направление соответствующего ей вектора поля
имеет направление соответствующего ей вектора поля 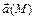 . Векторные линии поля
. Векторные линии поля 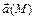 находятся из системы дифференциальных уравнений
находятся из системы дифференциальных уравнений
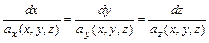 .
.
Если 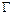 - плоская кусочно-гладкая простая (без точек самопересечений) замкнутая кривая, нигде не касающаяся векторных линий поля
- плоская кусочно-гладкая простая (без точек самопересечений) замкнутая кривая, нигде не касающаяся векторных линий поля 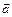 , то поверхность, образованная векторными линиями, пересекающими
, то поверхность, образованная векторными линиями, пересекающими 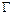 , называется векторной трубкой поля
, называется векторной трубкой поля 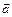 .
.
Дивергенцией векторного поля 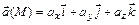 называется скалярная величина
называется скалярная величина 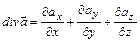 .
.
Ротором (вихрем) векторного поля 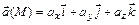 называется вектор
называется вектор 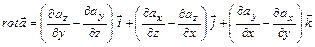 .
.
Все операции векторного анализа можно выразить при помощи оператора Гамильтона – символического вектора 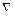 (читается - набла), определяемого равенством
(читается - набла), определяемого равенством 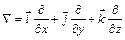 . Так, например:
. Так, например: 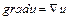 ,
, 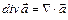 ,
, 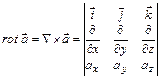 .
.
Оператором Лапласа (лапласианом) называется скалярный символ 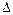 , определяемый равенством
, определяемый равенством 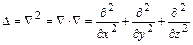 .
.
11.95 Найти векторные линии плоского векторного поля 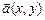 :
:
а) 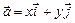 ; б)
; б) 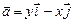 ; в)
; в) 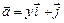 ; г)
; г) 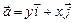 .
.
11.96 Найти векторные линии пространственного векторного поля 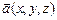 :
:
а) 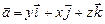 ; б)
; б) 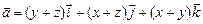 .
.
11.97 Вычислить 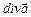 (
(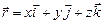 ,
, 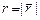 ): если:
): если:
а) 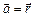 ; б)
; б) 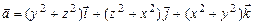 ;
;
в) 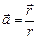 ; г)
; г) 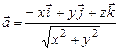 .
.
11.98 Вычислить 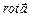 (
(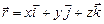 ,
, 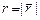 ): если:
): если:
а) 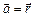 ; б)
; б) 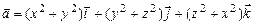 ;
;
в) 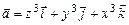 ; г)
; г) 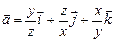 .
.
11.99 Доказать следующие соотношения:
а) 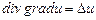 ; б)
; б) 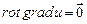 ; в)
; в) 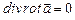 ;
;
г) 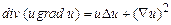 ; д)
; д) 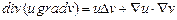 ;
;
е) 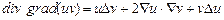 .
.
11.100 Найти 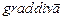 , если
, если 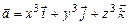 .
.
11.101 Найти 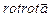 , если
, если 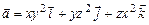 .
.
11.102 Найти 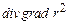 . 11.103 Найти
. 11.103 Найти 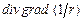 .
.
 2015-03-20
2015-03-20 597
597








