Линейным интегралом от вектора 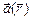 по кусочно-гладкой ориентированной кривой
по кусочно-гладкой ориентированной кривой 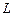 (работой
(работой 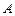 поля вдоль
поля вдоль 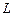 ) называется число
) называется число 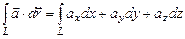 . Если кривая
. Если кривая 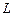 - замкнутая, то линейный интеграл называется циркуляцией
- замкнутая, то линейный интеграл называется циркуляцией 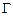 векторного поля
векторного поля 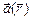 вдоль
вдоль 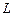 и обозначается
и обозначается 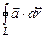 .
.
Если замкнутая кусочно-гладкая кривая 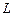 , ограничивает двустороннюю поверхность
, ограничивает двустороннюю поверхность 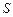 , то справедлива формула Стокса
, то справедлива формула Стокса
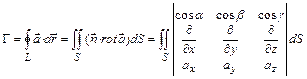 ,
,
где 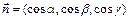 - единичный вектор нормали к поверхности
- единичный вектор нормали к поверхности 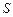 , направление которого выбирается так, чтобы для наблюдателя, смотрящего по направлению
, направление которого выбирается так, чтобы для наблюдателя, смотрящего по направлению  , обход контура
, обход контура 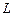 совершался против хода часовой стрелки.
совершался против хода часовой стрелки.
Если замкнутая кусочно-гладкая поверхность 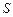 , ограничивает объём
, ограничивает объём 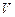 , то справедлива формула Гаусса-Остроградского
, то справедлива формула Гаусса-Остроградского
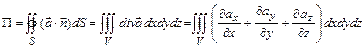 ,
,
где 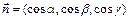 - единичный вектор внешней нормали к поверхности
- единичный вектор внешней нормали к поверхности 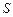 .
.
В задачах 11.108-11.111 используя формулу Стокса, найти циркуляцию 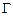 векторного поля
векторного поля 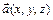 вдоль контура
вдоль контура 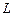 , ориентированного против хода часовой стрелки:
, ориентированного против хода часовой стрелки:
11.108 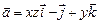 ,
, 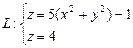 .
.
11.109 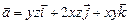 ,
, 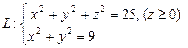 .
.
11.110 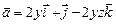 ,
, 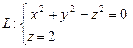 .
.
11.111 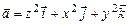 ,
, 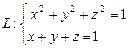 .
.
В задачах 11.112-11.115 найти работу 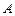 силового поля
силового поля 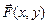 вдоль кривой
вдоль кривой 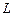 :
:
11.112 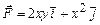 ,
, 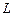 - наименьшая дуга окружности
- наименьшая дуга окружности 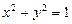 от точки
от точки 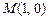 до точки
до точки 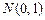 .
.
11.113 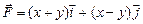 ,
, 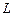 - часть графика
- часть графика 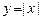 от точки
от точки 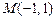 до точки
до точки 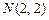 .
.
11.114 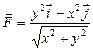 ,
, 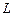 - полуокружность
- полуокружность 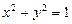 от точки
от точки 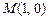 до точки
до точки 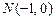 .в области
.в области 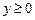 .
.
11.115 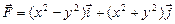 ,
, 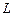 - дуга эллипса
- дуга эллипса 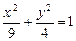 (
(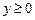 ) от точки
) от точки 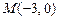 до точки
до точки 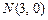 .
.
В задачах 11.116-11.117 найти поток 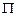 векторного поля
векторного поля 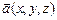 через ориентированную нормалью
через ориентированную нормалью  поверхность
поверхность 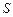 :
:
11.116 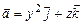 ,
, 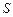 - часть внешней стороны параболоида
- часть внешней стороны параболоида 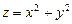 , отсечённая плоскостью
, отсечённая плоскостью 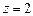 .
.
11.117 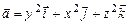 ,
, 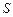 - часть внешней стороны цилиндра
- часть внешней стороны цилиндра 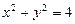 , расположенная в первом октанте между плоскостями
, расположенная в первом октанте между плоскостями 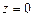 и
и 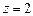 .
.
11.118 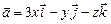 ,
, 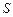 - часть внешней стороны параболоида
- часть внешней стороны параболоида 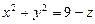 , расположенная в первом октанте.
, расположенная в первом октанте.
11.119 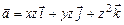 ,
, 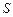 - часть внешней стороны сферы
- часть внешней стороны сферы 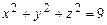 , расположенная в области
, расположенная в области 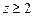 .
.
В задачах 11.120-11.123, используя формулу Гаусса-Остроградского, найти поток 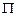 векторного поля
векторного поля 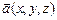 через замкнутую поверхность
через замкнутую поверхность 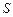 :
:
11.120 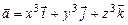 ,
, 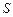 - полная внешняя поверхность куба:
- полная внешняя поверхность куба: 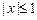 ,
, 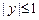 ,
, 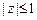 .
.
11.121 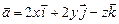 ,
, 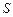 - полная внешняя поверхность конуса
- полная внешняя поверхность конуса 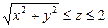 .
.
11.122 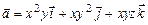 ,
, 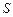 - полная внешняя поверхность тела
- полная внешняя поверхность тела 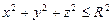 ,
, 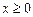 ,
, 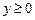 ,
, 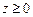 .
.
11.123 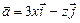 ,
, 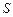 - полная внешняя поверхность тела
- полная внешняя поверхность тела 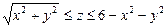 .
.
 2015-03-20
2015-03-20 1325
1325







