Теория поля.
Пусть 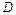 - область в двумерном пространстве. Скалярным полем на
- область в двумерном пространстве. Скалярным полем на 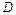 называется числовая функция
называется числовая функция 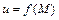 , заданная в точках
, заданная в точках 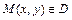 . Линии
. Линии 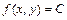 , где
, где 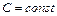 называются линиями уровня скалярного поля
называются линиями уровня скалярного поля 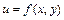 .
.
Пусть 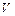 - область в трёхмерном пространстве.
- область в трёхмерном пространстве.
Скалярным полем на 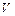 называется числовая функция
называется числовая функция 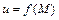 , заданная в точках
, заданная в точках 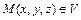 . Поверхности
. Поверхности 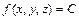 , где
, где 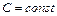 называются поверхностями уровня скалярного поля
называются поверхностями уровня скалярного поля 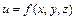 .
.
Градиентом скалярного поля 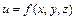 называется вектор
называется вектор
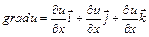 .
.
Производная скалярного поля 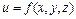 по направлению произвольного вектора
по направлению произвольного вектора 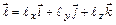 вычисляется по формуле
вычисляется по формуле  , где
, где 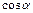 ,
, 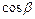 ,
, 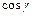 - направляющие косинусы вектора
- направляющие косинусы вектора 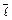 .
.
Градиент скалярного поля 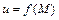 в точке
в точке 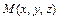 направлен по нормали к поверхности уровня
направлен по нормали к поверхности уровня 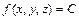 , проходящей через
, проходящей через 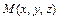 в сторону возрастания поля, а его модуль
в сторону возрастания поля, а его модуль 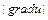 равен наибольшей производной по направлению в этой точке.
равен наибольшей производной по направлению в этой точке.
11.81 Найти линии уровня следующих скалярных полей:
а) 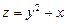 ; б)
; б) 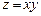 ; в)
; в) 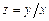 ; г)
; г) 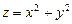 .
.
11.82 Найти поверхности уровня следующих скалярных полей:
а) 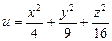 ; б)
; б) 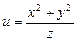 ;
;
в) 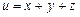 ; г)
; г) 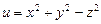 .
.
11.83 Найти градиент скалярного поля 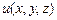 в точке
в точке 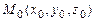 , если:
, если:
а) 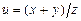 ,
, 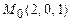 ; б)
; б) 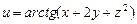 ,
, 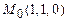 .
.
11.84 Найти угол 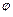 между градиентами скалярного поля
между градиентами скалярного поля 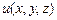 в точках
в точках 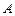 и
и 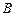 , если:
, если:
а) 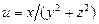 ,
, 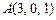 ,
, 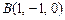 ;
;
б) 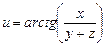 ,
, 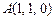 ,
, 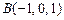 .
.
11.85 Найти, полагая 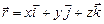 ,
, 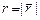 :
:
а) 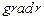 ; б)
; б) 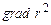 ; в)
; в) 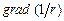 ; г)
; г) 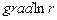 .
.
11.86 Найти точки в которых градиент скалярного поля 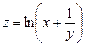 равен вектору
равен вектору 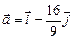 .
.
11.87 Найти точки в которых градиент скалярного поля 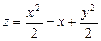 перпендикулярен радиус-вектору
перпендикулярен радиус-вектору 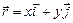 .
.
11.88 Найти точки в которых модуль градиента скалярного поля 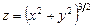 равен 2.
равен 2.
11.89 Найти стационарные точки скалярного поля 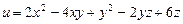 .
.
11.90 Найти единичный вектор нормали к поверхности уровня скалярного поля 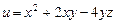 в точке
в точке 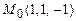 , направленный в сторону возрастания поля.
, направленный в сторону возрастания поля.
11.91 Найти производную скалярного поля 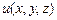 по направлению вектора
по направлению вектора 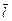 в точке
в точке 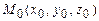 , если:
, если:
а) 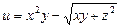 ,
, 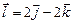 ,
, 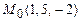 ;
;
б) 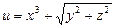 ,
,  ,
,  .
.
11.92 Найти производную скалярного поля 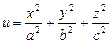 в точке
в точке 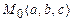 по направлению радиус-вектора
по направлению радиус-вектора 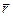 этой точки.
этой точки.
11.93 Найти производную скалярного поля 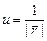 в точке
в точке 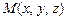 по направлению его градиента (
по направлению его градиента (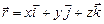 -радиус вектор точки
-радиус вектор точки 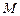 ).
).
11.94 Найти скорость и направление наибыстрейшего возрастания скалярного поля 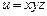 в точке
в точке 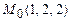 .
.
 2015-03-20
2015-03-20 1309
1309