Векторное поле 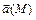 называется потенциальным, если
называется потенциальным, если 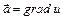 , где
, где 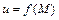 -скалярная функция (потенциал векторного поля).
-скалярная функция (потенциал векторного поля).
Для потенциальности векторного поля 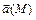 , заданного в односвязной области, необходимо и достаточно, чтобы оно было безвихревым, т.е. чтобы
, заданного в односвязной области, необходимо и достаточно, чтобы оно было безвихревым, т.е. чтобы  . В этом случае существует потенциал поля
. В этом случае существует потенциал поля 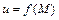 , который может быть вычислен по формуле
, который может быть вычислен по формуле 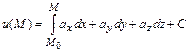 , где
, где 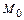 - некоторая фиксированная точка. Для вычисления интеграла можно выбрать любой путь, соединяющий точки
- некоторая фиксированная точка. Для вычисления интеграла можно выбрать любой путь, соединяющий точки 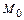 и
и 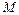 . Наиболее простым является путь, составленный из эвеньев ломаной, параллельных осям координат, причём за точку
. Наиболее простым является путь, составленный из эвеньев ломаной, параллельных осям координат, причём за точку 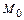 , если это возможно, удобно принимать начало координат.
, если это возможно, удобно принимать начало координат.
Векторное поле 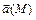 называется соленоидальным, если в каждой точке поля
называется соленоидальным, если в каждой точке поля 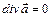 . Для соленоидального поля поток вектора через любую замкнутую поверхность равен нулю.
. Для соленоидального поля поток вектора через любую замкнутую поверхность равен нулю.
Векторное поле 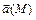 , в каждой точке которого
, в каждой точке которого  и
и 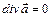 , называется гармоническим.
, называется гармоническим.
11.104 Проверить, является ли векторное поле 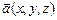 потенциальным?
потенциальным?
а) 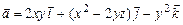 ; б)
; б) 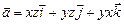 ;
;
в) 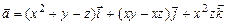 ;
;
г) 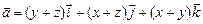 .
.
11.105 Найти потенциал векторного поля 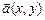 :
:
а) 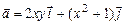 ; б)
; б) 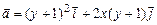 .
.
11.106 Проверить, является ли векторное поле 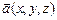 соленоидальным?
соленоидальным?
а) 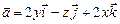 ; б)
; б) 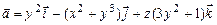 ;
;
в) 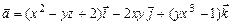 ;
;
г) 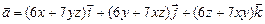 .
.
11.107 Проверить, является ли векторное поле 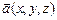 гармоническим? (
гармоническим? (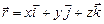 ,
, 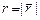 )
)
а) 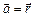 ; б)
; б) 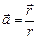 ; в)
; в) 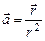 ; г)
; г) 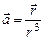 .
.
 2015-03-20
2015-03-20 1524
1524
