Если функция 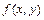 непрерывна в неограниченной области
непрерывна в неограниченной области 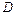 , то по определению полагают
, то по определению полагают 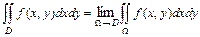 , где
, где 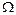 - ограниченная замкнутая область, которая целиком лежит в области
- ограниченная замкнутая область, которая целиком лежит в области 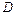 и стремится к
и стремится к 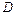 произвольным образом. Если предел в правой части существует и не зависит от выбора области
произвольным образом. Если предел в правой части существует и не зависит от выбора области 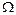 , то соответствующий несобственный интеграл по бесконечной области называется сходящимся, в противном случае расходящимся. Предел в правой части не зависит от выбора
, то соответствующий несобственный интеграл по бесконечной области называется сходящимся, в противном случае расходящимся. Предел в правой части не зависит от выбора 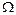 , если
, если 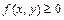 в области
в области 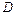 .
.
Если функция 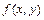 непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области 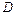 всюду, за исключением точки
всюду, за исключением точки 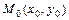 , то по определению полагают
, то по определению полагают 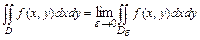 , где
, где 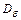 - область, получаемая из
- область, получаемая из 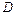 путём удаления малой области диаметра
путём удаления малой области диаметра 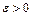 , содержащей точку
, содержащей точку 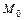 . Если предел в правой части существует и не зависит от вида удаляемых из
. Если предел в правой части существует и не зависит от вида удаляемых из 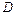 малых областей, то соответствующий несобственный интеграл от разрывной функции называется сходящимся, в противном случае расходящимся. Предел в правой части не зависит от вида удаляемых из
малых областей, то соответствующий несобственный интеграл от разрывной функции называется сходящимся, в противном случае расходящимся. Предел в правой части не зависит от вида удаляемых из 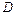 малых областей, если
малых областей, если 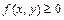 в области
в области 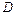 и в этом случае, в качестве таких областей можно брать круги радиуса
и в этом случае, в качестве таких областей можно брать круги радиуса 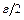 с центром в точке
с центром в точке 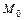 .
.
Аналогично определяется несобственный интеграл, если функция 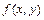 в ограниченной замкнутой области
в ограниченной замкнутой области 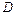 имеет линию разрыва
имеет линию разрыва 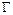 . В этом случае
. В этом случае 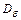 - область, получаемая из
- область, получаемая из 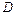 путём удаления полосы малой ширины
путём удаления полосы малой ширины 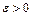 , содержащей линию разрыва
, содержащей линию разрыва 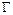 .
.
В задачах 10.143-10.154 вычислить несобственные интегралы по бесконечной области или установить их расходимость:
10.143 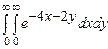 . 10.144
. 10.144 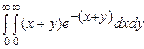 .
.
10.145 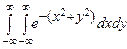 . 10.146
. 10.146 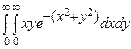 .
.
10.147 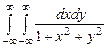 . 10.148
. 10.148 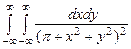 .
.
10.149 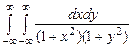 . 10.150
. 10.150 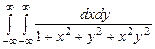 .
.
10.151 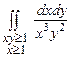 . 10.152
. 10.152 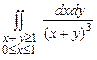 .
.
10.153 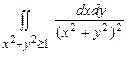 . 10.154
. 10.154 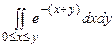 .
.
В задачах 10.155-10.160 вычислить несобственные интегралы от разрывных функций или установить их расходимость:
10.155 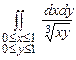 . 10.156
. 10.156 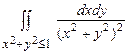 .
.
10.157 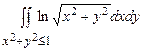 . 10.158
. 10.158 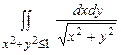 .
.
10.159 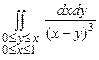 . 10.160
. 10.160 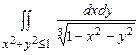 .
.
 2015-03-20
2015-03-20 793
793








