2015-03-20
259
§1. Криволинейный интеграл первого рода и его приложения.
Если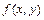 
- функция, определённая и непрерывная в точках гладкой плоской кривой 
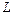, заданной уравнением 
(
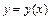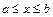) и 
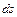- дифференциал дуги, то криволинейный интеграл 1-го рода вычисляется по формуле 
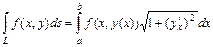. В случае параметрического задания кривой : 
, 
(
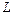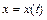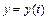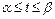) имеет место формула 
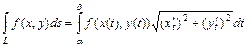. Если плоская кривая 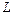задана уравнением 
(
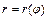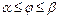) в полярных координатах, то 
.
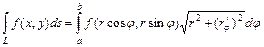Если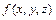 
- функция, определённая и непрерывная в точках гладкой пространственной кривой : , , 
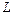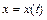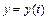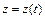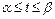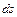() и - дифференциал дуги, то криволинейный интеграл 1-го рода вычисляется по формуле
.
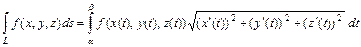Особенность криволинейного интеграла 1-го рода состоит в том, что он не зависит от направления пути интегрирования.
Длина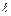 
дуги кривой 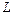вычисляется по формуле 
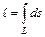. Масса 
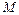дуги кривой 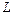с плотностью 
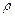вычисляется по формуле 
.
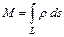Если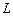 
- дуга плоской кривой с плотностью 
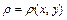, то её статические моменты 
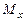и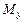 
, моменты инерци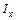и 
и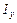 
относительно осе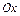й 
и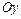 
, координаты 
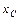и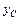 
центра масс 
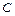вычисляются
по формулам:
