Тройной интеграл

Пусть функция 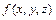непрерывна в ограниченной замкнутой пространственной области 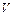. Если область 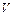имеет вид 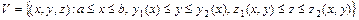, где функции 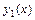, 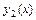- непрерывны и заданы одним аналитическим выражением на отрезке 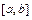, функции 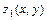, 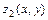- непрерывны и заданы одним аналитическим выражением в области 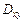, являющейся проекцией области 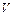на плоскость 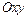, то выражение 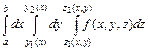называется повторным интегралом от функции 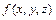по области 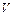. Аналогично вводятся другие повторные интегралы.

В повторных интегралах от функции 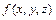последовательно вычисляются простые (однократные) интегралы, причём интегрирование производится по внутренней переменной, а внешние переменные считаются постоянными. В результате последовательных интегрирований получим число.

В задачах 10.81-10.88 вычислить повторные интегралы:

10.81 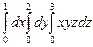. 10.82 .

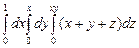10.83 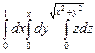. 10.84 .

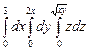10.85 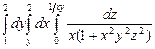. 10.86 .

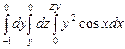10.87 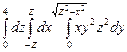. 10.88 .

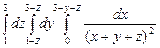Тройным интегралом от непрерывной функции 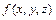по ограниченной замкнутой пространственной области 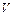называется число 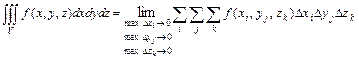, где 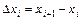, , 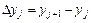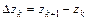и суммирование ведётся по тем значениям 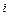, 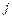и 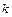, для которых .

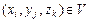Замкнутую область 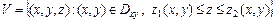, где функции 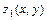, 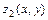- непрерывны и заданы одним аналитическим выражением в области 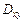, являющейся проекцией области 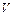на плоскость 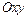, будем называть элементарной в направлении оси 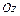и обозначать 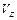. Аналогично вводятся элементарные области в направлении других координатных осей.

Вычисление тройного интеграла сводится к последовательному вычислению одного двойного интеграла и одного простого (однократного) или к вычислению трёх простых интегралов.

Тройной интеграл по области 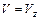вычисляется по формуле

.

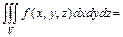
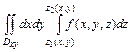Если область 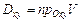- элементарная в направлении оси 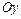, т.е. имеет вид 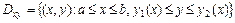, где функции 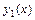, 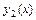- непрерывны и заданы одним аналитическим выражением на отрезке 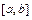, то применяют формулу

.

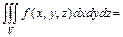
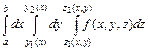Если область 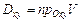- элементарная в направлении оси 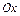, т.е. имеет вид 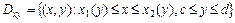, где функции 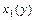, 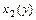- непрерывны и заданы одним аналитическим выражением на отрезке 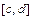, то применяют формулу

.

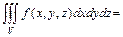
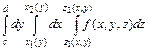Если 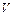не является элементарной, то её представляют в виде объединения непересекающихся (без общих внутренних точек) областей 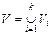, каждая из которых является элементарной в направлении той или другой координатной оси. Разбиение зависит от желаемого порядка расстановки пределов интегрирования. Тогда в силу аддитивности тройного интеграла .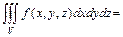

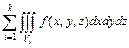В задачах 10.89-10.94 вычислить тройные интегралы по областям 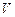, ограниченными указанными поверхностями:

10.89 , . , , , .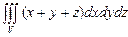

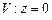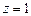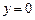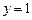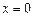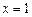10.90 , . , , , .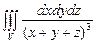

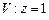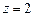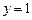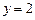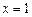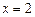10.91 , . , .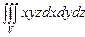

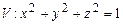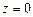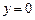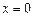10.92 , .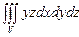

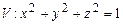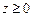10.93 , , , , .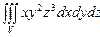

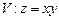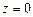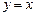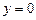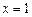10.94 , , , , .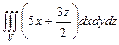

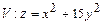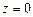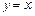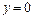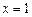При переходе в тройном интеграле от прямоугольных координат 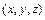к цилиндрическим координатам 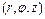, связанным с прямоугольными координатами соотношениями 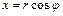, , 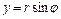, 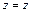имеет место формула

,

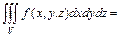
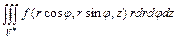где 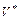-область интегрирования в пространстве переменных 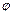, 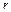и .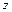

Если область 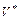имеет вид 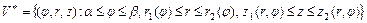, то применяют формулу

.

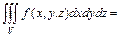
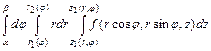При переходе в тройном интеграле от прямоугольных координат 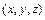к сферическим координатам 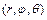( 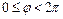-долгота, 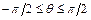-широта) связанным с прямоугольными координатами соотношениями 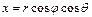, , 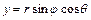, 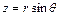имеет место формула

,

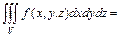
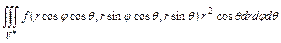где 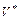-область интегрирования в пространстве переменных 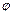, 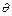и .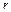

Если область 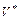имеет вид 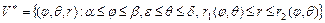, то применяют формулу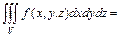 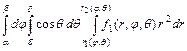, где .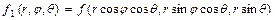

В задачах 10.95-10.98 в тройном интеграле 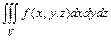перейти к цилиндрическим координатам 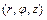, и расставить пределы интегрирования:

10.95 .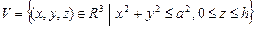

10.96 .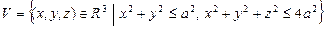

10.97 .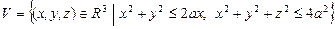

10.98 .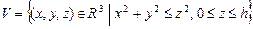

В задачах 10.99-10.102 в тройном интеграле 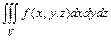перейти к сферическим координатам 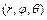, и расставить пределы интегрирования:

10.99 .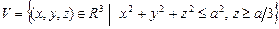

10.100 .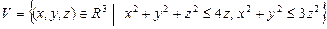

10.101 .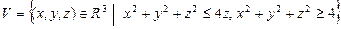

10.102 .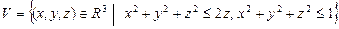

В задачах 10.103-10.108 перейти к цилиндрическим координатам и вычислить следующие тройные интегралы:

10.103 , , , .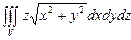

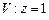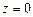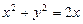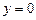10.104 , .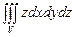

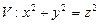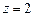10.105 , .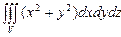

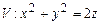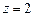10.106 , , .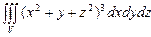

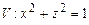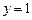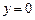10.107 , , .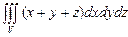

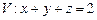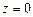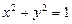10.108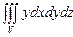

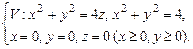
В задачах 10.109-10.112 перейти к сферическим координатам и вычислить следующие тройные интегралы:

10.109 .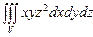

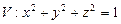
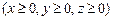10.110 .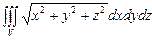

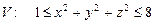10.111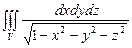

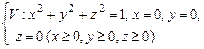
10.112 .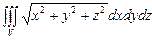

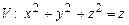§4. Некоторые приложения тройного интеграла.

Объём υ тела 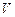вычисляется по формуле υ .

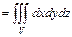Среднее значение непрерывной функции 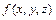в пространственной области 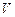вычисляется по формуле .

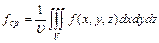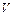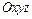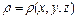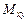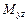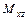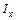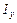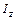Если - область пространства , занятого телом, и - плотность тела, то статические моменты тела относительно координатных плоскостей , и , моменты инерции тела относительно координатных осей , и , моменты инерции тела относительно координатных плоскосте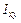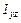й , и 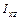, масса 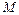тела, координаты 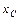, , 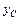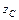центра масс 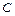тела вычисляются по формулам:

, , ,

, , ,

, , , , , , .

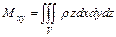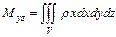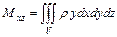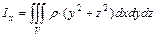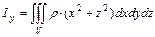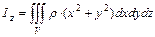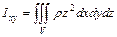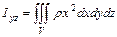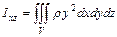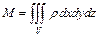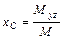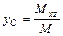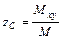Если тело однородное, то полагают .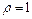

В задачах 10.113-10.116 найти объём тела 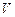, ограниченного указанными поверхностями:

10.113 , , , .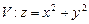

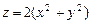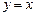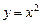10.114 , , , , .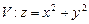

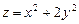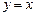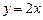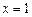10.115 , , , , .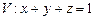

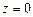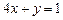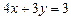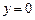10.116 , .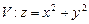

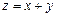В задачах 10.117-10.120 перейти к цилиндрическим координатам и найти объём тела 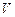, ограниченного поверхностями:

10.117 , .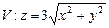

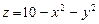10.118 , .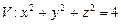

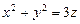
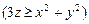10.119 , .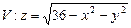

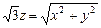10.120 , .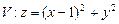

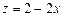В задачах 10.121-10.122 перейти к сферическим координатам и найти объём тела 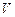, ограниченного поверхностями:

10.121 , , ,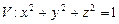

.

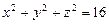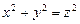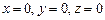
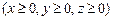10.122 , .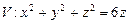

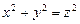
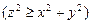10.123 Найти среднее значение функции 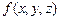в области :

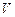а) ;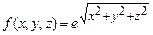

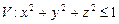б) .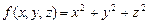

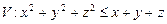В задачах 10.124-10.127 найти массу тела 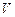плотности 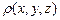, ограниченного поверхностями:

10.124 , , , .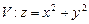

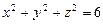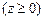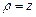10.125 , , .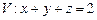

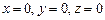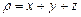10.126 , , .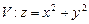

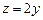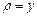10.127 , , , .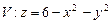

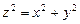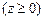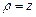10.128 Найти массу куба с ребром 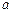, если его плотность 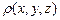в каждой точке равна квадрату расстояния этой точки до одной из вершин куба.

10.129 Найти массу прямого кругового цилиндра, высота которого равна 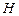, а радиус основания 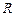, если его плотность 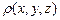в каждой точке равна квадрату расстояния этой точки от центра основания цилиндра.

10.130 Найти массу и среднюю плотность сферического слоя между поверхностям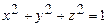и и 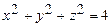, если его плотность 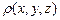в каждой точке пропорциональна квадрату расстояния от точки до начала координат, а наибольшее значение плотности .

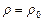В задачах 10.131-10.134 найти координаты центра масс однородного тела 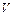плотности 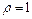, ограниченного поверхностями:

10.131 , .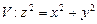

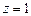10.132 , , .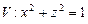

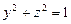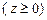10.133 , , , .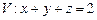

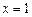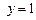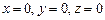10.134 , , .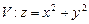

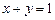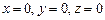В задачах 10.135-10.137 найти момент инерции относительно указанной оси однородного тела 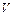плотности 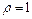, ограниченного следующими поверхностями:

10.135 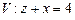, , 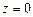, 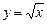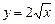относительно .

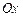10.136 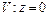, , 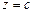, , 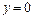, 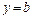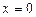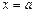относительно .

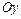10.137 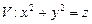, 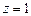относительно .

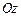В задачах 10.138-10.140 найти момент инерции относительно указанной плоскости однородного тела 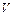плотности 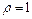, ограниченного следующими поверхностями:

10.138 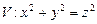, 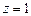относительно .

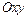10.139 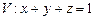, , 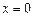, 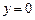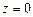относительно .

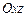10.140 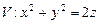, 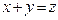относительно .

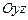10.141 Найти момент инерции однородного сегмента параболоида вращения плотности 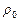с радиусом основания 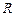и высотой 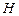относительно его оси вращения.

10.142 Найти момент инерции однородного кругового конуса плотности 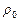с радиусом основания 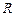и высотой 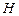относительно его оси.