Общее уравнение: 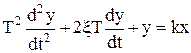
Характеристическое уравнение
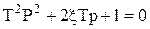
Корни уравнения
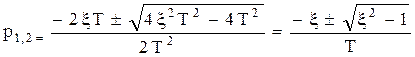
1. Если 0<ξ<1, то корни – комплексные, звено называется колебательным.
2. Если 1≤ξ, то корни действительные, звено – апериодическое 2-го порядка.
3. Если ξ=0, корни чисто мнимые – звено называется консервативное.
ξ –коэффициент демпфирования, т.е. коэффициент сглаживания пульсаций.
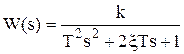 - передаточная функция.
- передаточная функция.
VI. 1. Колебательное звено.
0<ξ<1
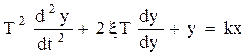
3.h(t)
y(t)=yобщ(t)+yчастн.(t), x=1(t), y(0)=0; y`(0)=0.
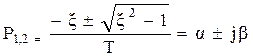 ,
,
где 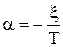 ,
, 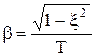 .
.
Общее решение в данном случае: yобщ=Сeαtsin(βt+γ), yч=к1(t)
y(t)=(Сeαtsin(βt+γ)+к)1(t)
y(0)=C sin(γ)+к=0
y`(0)=|αCeαt sin(βt+γ)+ βСeαtcos(βt+γ)|= αC sin(γ)+βСcos(γ)=0
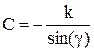 ,
, 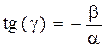 ,
, 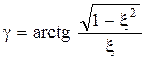

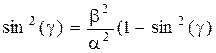
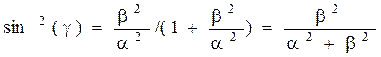
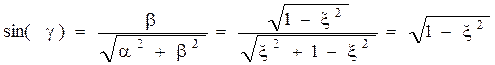

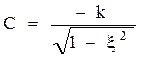
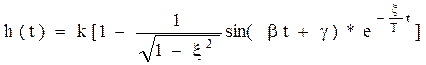
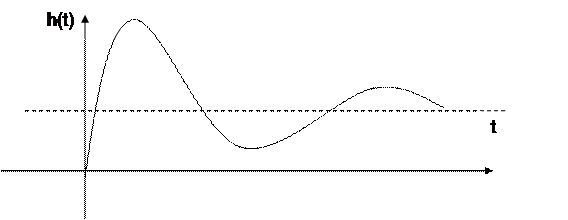 |
β- частота колебаний.
α-определяет скорость затухания колебаний, причем чем меньше
время T, тем быстрее затухают колебания, и чем больше ξ тем быстрее
затухают колебания
4.
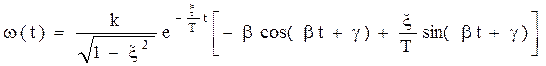

|


|
5.
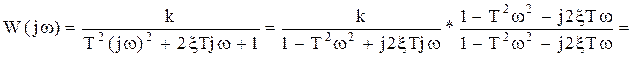
|
|


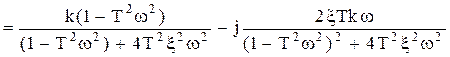
|
|


|
6. 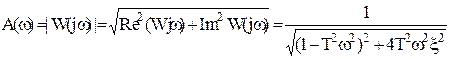

Причем 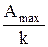 - будет тем больше, чем меньше ξ.
- будет тем больше, чем меньше ξ.
ω* - называется резонансной частотой; коэффициент усиления на этой
частоте максимальный.
7. 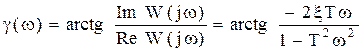
 | |||
| |||


|
|


8. ЛАХ
|
|
|

|


|
|
|
|




|
|
 |
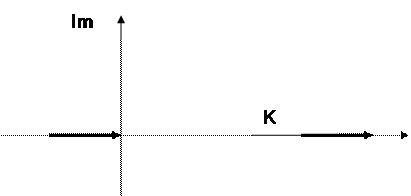
VII. ξ=0, консервативное звено.
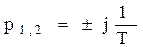 ,
, 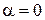 ,
, 
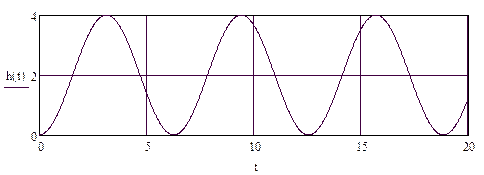
3. y(t)=(Сsin(βt+γ)+k)1(t)
Из начальных условий: Csin(γ)+k=0, 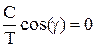
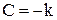
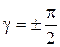
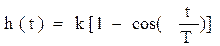
|
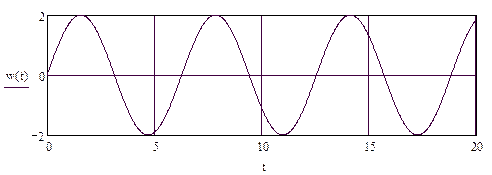
4. 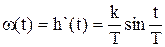
|
5. 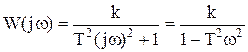
|
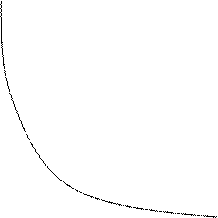

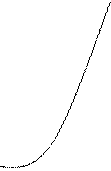 6.
6. 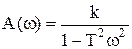
 | |||
|
7. 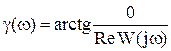
 |

 8. ЛАХ
8. ЛАХ
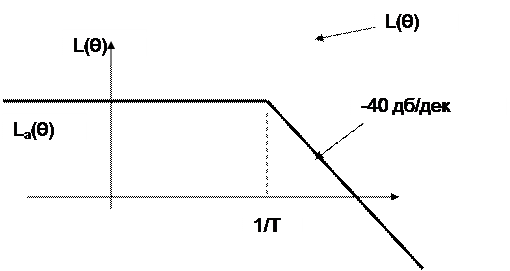
ξ≥1, апериодическое звено 2-го порядка
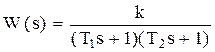 , где T1*T2=T2, T1+ T2=2ξT
, где T1*T2=T2, T1+ T2=2ξT
Последовательное соединение 2-х апериодических звеньев 1-го порядка.
3. h(t)=k(C1e-t/T+ C2e-t/T+1)
|



|
|

Кривая 2-го порядка имеет перегиб.
В начале производная должна быть равна 0, а за тем “+”.
|


|
4. Частотные характеристики рассматриваются далее…
IX. Неминимальнофазовые звенья
Звено первого порядка
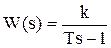
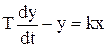
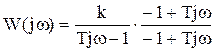 =
= 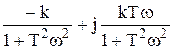
АЧХ – как у апериодического звена.
Комплексная частотная характеристика:
|


|
|

| |||
 | |||
|
|




X Звено транспортного запаздывания.
1. y(t)=kx(t-τ) (конвейер, труба)
2. W(S)=kesτ
3. h(t)=k1(t- τ)
4. ω(t)=kδ(t- τ)
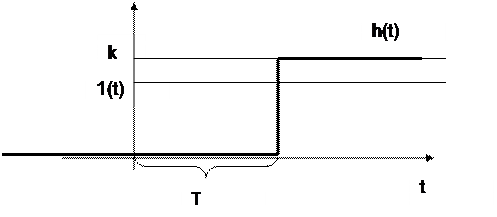 |
5. W(jω)=k*e-jωτ=k(cos(ωt)-jsin(ωt))
|


|

|
6. A(ω)=k
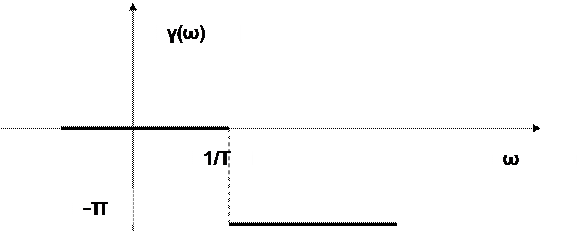
γ (ω)=-ωτ

|

|

Лекция 7
 2015-03-20
2015-03-20 443
443








