Идентификация объекта по каналам управления и возмущения

Основой математического аппарата синтеза ЦСУ являются разностные схемы [7]. При этом каждый из каналов ОУ описывается разностным уравнением, которое с учетов векторной формы записи может быть представлено в следующем виде:

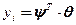(4.18)

где u_i, y_i – вход и выход ОУ;

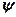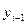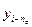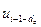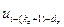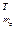=[ ,…, , ,…, ] – вектор переменных состояния;

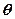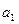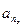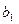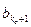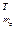=[ ,…, , ,…, ] – вектор параметров разностного уравнения;

d_о = τ_о / T' ₀ – целое число тактов запаздывания;

τ_о – время запаздывания;

T' ₀ – такт квантования;

n_о, k_о – порядки знаменателей и числителей дискретных передаточных функций каналов ОУ (n_о≥k_о);

m_о = n_о+k_о +1 – число переменных состояния каналов ОУ;

i – индекс такта квантования.

Широко применяемым для идентификации линейных и нелинейных объектов (систем) является метод наименьших квадратов (МНК), позволяющий обеспечить высокую адекватность получаемых моделей. Суть его заключается в нахождении таких параметров модели, при которых сумма квадратичных отклонений между экспериментальными значениями выхода объекта и рассчитанными по модели была минимальной:

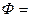
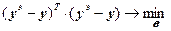, (4.19)

где 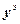=[ 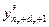,…, 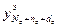] 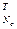– вектор экспериментальных значений выхода ОУ, полученных путем измерения через равные промежутки времени T' ₀ при снятии кривой разгона; 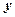=[ 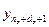,…, 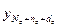] 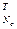– вектор значений выхода ОУ, рассчитанных по модели (4.18);

N_о – объем выборки при идентификации.

Поскольку вектор 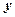, с учетом (4.18), может быть представлен соотношением:

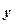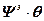= , (4.20)

то (4.19) примет вид:

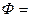
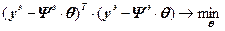, (4.21)

где 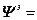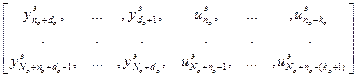– матрица экспериментальных значений, N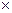_о m_о.

Так как квадратичная функция 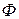относительно вектора неизвестных параметров 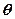ограничена снизу, то точка минимума существует и является решением системы линейных уравнений:

2· 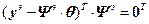или 2· 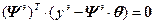, (4.22)

где 0= [0,…,0] 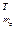– нулевой вектор.

Если матрица (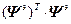) не вырождена, то решение единственно. Необходимое условие для выполнения данного требования – входной сигнал представляет собой возбуждающий процесс порядка не ниже n_о, т.е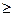. N_о n_о.

Выполнив преобразования, приведем уравнения (4.22) к нормальному виду:

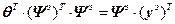или

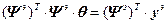. (4.23)

Решая нормализованное уравнение (4.23), или соответствующую систему линейных уравнений (например, методом Гаусса), можно найти параметры (коэффициенты) разностного уравнения (4.18).

В векторно-матричной форме решение имеет вид:

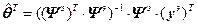или

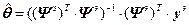, (4.24)

где 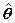=[ 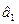,…, , 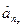,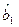…, 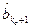] 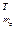– вектор оценок неизвестных параметров.

Полученные таким образом оценки параметров 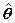с помощью МНК не смещены (М (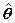)= )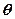, эффективны ( 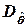=diag[( 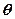- 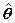) ( 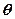- 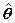) ^Т ]→min) и состоятельны, поскольку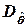 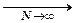0.

Оптимальная с точки зрения минимума среднеквадратичной ошибки оценка выходной переменной y_i записывается в виде:

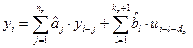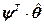= . (4.25)

Расчет параметров a_j (j = 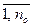), b_l (l = 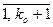) удобнее проводить не в абсолютных значениях, а в приращениях (вариациях), т.е. значение входа и выхода в установившемся состоянии перед нанесением входного воздействия (до начала эксперимента) принимаются равными нулю. После начала эксперимента, когда на вход подано воздействие, значение входа и выхода определяются как приращения.

Адекватность дискретных моделей различных порядков определяется по критерию Фишера. При отсутствии параллельных опытов модель адекватна ОУ, если расчетный критерий Фишера F_р больше критического значения F_табл (p, f ₁, f ₂):

F_р > F_табл (p, f ₁, f ₂), (4.26)

а при наличии параллельных опытов, если расчетный критерий Фишера F_р^пар меньше критического значения 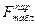(p, f ₁, f ₂):

F_р^пар < 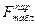(p, f ₁, f ₂). (4.27)

Критическое значение Фишера выбирается из таблиц распределения Фишера при выбранном уровне значимости.

В результате идентификации определяются порядки n_о, k_о и значения параметров a_j (j = 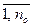), b_l (l = 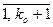) разностных уравнений (моделей) каналов ОУ, которые используются на этапе синтеза управляющей части системы и исследования.