2015-03-20
623
Использование первого подхода для синтеза связанной ЦСУ предполагает выполнение в качестве первого этапа расчет цифровых компенсаторов перекрестных связей из условия автономности.
Далее покажем, что для объекта любой размерности (r> 2) расчет передаточных функций компенсаторов перекрестных связей будет осуществляться по совершенно другим зависимостям, отличающимся от рассмотренного в разделе 2.6 двумерного случая.
Более того, выражения для расчета передаточных функций компенсаторов, удовлетворяющих условию автономности, зависят от размерности объекта управления и для каждого конкретного r имеют свой определенный вид.
Поэтому возникает задача получения такого универсального алгоритма расчета компенсаторов, который может быть применен для систем высокого порядка (r> 2) на основе матричной формы описания многомерного объекта.
Рассмотрим r -мерную систему (рис. 4.5) связанного управления (r³ 2).
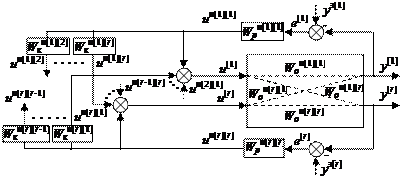
Рис. 4.5. Структурная схема системы связанного управления
r -мерным объектом (подход I)
|
|
|
В векторно-матричной форме система уравнений, описывающих ее поведение, имеет вид:
е = y з - y,
u u = W рu · е,
u = W кu · u u, (4.28)
y = W оu · u,
где е =[ е [1](z),…, е [ r ](z)] Т – вектор ошибок управления;
y з =[ yз [1](z),…, yз [ r ](z)] Т – вектор заданий;
y =[ y [1](z),…, y [ r ](z)] Т – вектор выходов ОУ;
и u =[ иu [1][1](z),…, иu [ r ][ r ](z)] Т – вектор выходов основных регуляторов;
и =[ и [1](z),…, и [ r ](z)] Т – вектор управляющих воздействий;
W оu – матрица дискретных передаточных функций объекта по основным и перекрестным каналам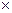, r 
r;
W рu, W кu – диагональная матрица дискретных передаточных функций регуляторов и матрица дискретных передаточных функций компенсаторов, r 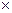r; z – оператор временного сдвига.
W оu =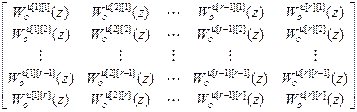 
;
W рu =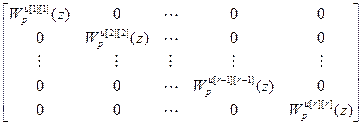 
;
W кu =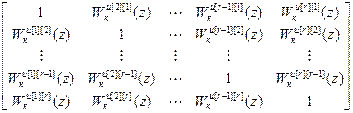 
.
= 
= 
=
= 
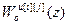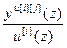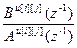
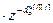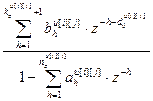– дискретная передаточная функция объекта по основным (i=j) и перекрестным (i ≠ j) каналам;
= 
= 
=
= 
=
= 
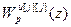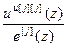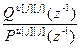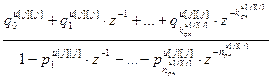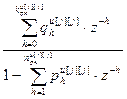– дискретная передаточная функция j -го регулятора;
= 
= 
=
= 
=
= 
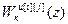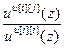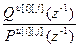
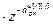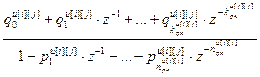
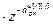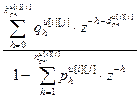– дискретная передаточная функция компенсатора перекрестной связи (i ≠ j);
, 
, 
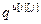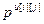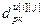– параметры и число тактов запаздывания дискретной передаточной функции регулятора (i=j) или компенсатора (i ≠ j);
, 
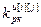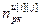– порядки числителя и знаменателя дискретной передаточной функции регулятора (i=j) или компенсатора (i≠j); uu [ i ][ j ](z) – выходы регуляторов (i=j) и компенсаторов (i≠j);
i, j =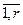 
.
Используя уравнения системы (4.28), выполним ряд преобразований:
y = W оu · W кu · W рu ·(y з - y),
y = W оu · W кu · W рu · y з - W оu · W кu · W рu · y,
y + W оu · W кu · W рu · y = W оu · W кu · W рu · y з,
(I + W оu · W кu · W рu)· y = W оu · W кu · W рu · y з,
y =(I + W оu · W кu · W рu)-1· W оu · W кu · W рu · y з, (4.29)
где I – единичная матрица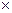, r r.
Уравнение (4.29) является решением (4.28) и позволяет определить функциональную зависимость выходов ОУ (элементов y) от входов системы (элементов y з).
|
|
|
Векторно-матричная форма записи позволяет получить в компактном виде условие автономности для системы (рис. 4.5).
Условие автономности выполняется, если матрица (I + W оu · W кu · W рu) – диагональная. Так как I – диагональная матрица, следовательно, и произведение (W оu · W кu · W рu) также должно быть диагональной матрицей, т.е. все недиагональные элементы равны нулю:
R = W оu · W кu · W рu, (4.30)
где R =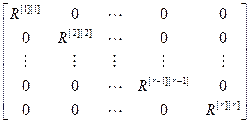 
– диагональная матрица, r 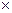r; diag[ R ]=diag[ W оu · W кu · W рu ].
Поскольку W рu – диагональная матрица, то из (4.30) следует, что матрица R будет диагональной в том случае, если произведение (W оu · W кu) также является диагональной матрицей.
Существует несколько подходов к диагонализации матрицы (W оu · W кu) при расчете компенсаторов.
=
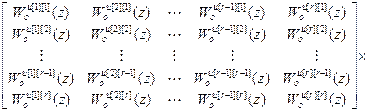
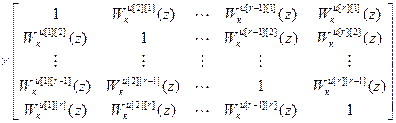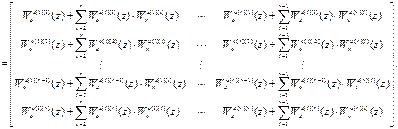
(4.31)
При первом подходе, приравнивая нулю недиагональные элементы полученной матрицы (на основании предъявляемого требования о диагональности), приходим к системе неоднородных линейных уравнений относительно искомых дискретных передаточных функций компенсаторов:
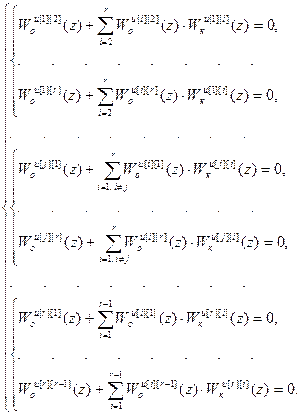(4.32)
Систему (4.32) можно представить векторно-матричным уравнением:
W оu авт · W кu авт + W оuu авт = 0, (4.33)
где W оu авт – блочная матрица, элементами которой являются матрицы дискретных передаточных функций основных и перекрестных каналов объекта;
W кu авт – блочный вектор, элементами которого являются векторы дискретных передаточных функций компенсаторов;
W оuu авт – блочный вектор, элементами которого являются векторы дискретных передаточных функций перекрестных каналов объекта;
0 – нулевой вектор, (r -1)· r.
W оu авт =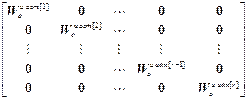 
;
W кu авт =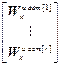 
; W оuu авт = 
,
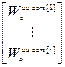где W оu авт [ i ] – матрица, получаемая из матрицы W оu вычеркиванием i -ой строки и i -го столбца, (r -1) 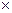(r -1);
W кu авт [ i ] – вектор, получаемый из i -го столбца матрицы W кu вычеркиванием i -ой строки, (r -1);
W оuu авт [ i ] – вектор, получаемый из i -го столбца матрицы W оu вычеркиванием i -ой строки, (r -1).
Если матрица W оu авт не вырождена, то существует единственное решение уравнения (4.33), определяемое по формуле:
W кu авт =-(W оu авт)-1· W оuu авт. (4.34)
Полученная зависимость (4.34) позволяет выполнить расчет дискретных передаточных функций компенсаторов из условия автономности.
Повышение числа управляемых величин объекта приводит к резкому увеличению размерности W оu авт. А поскольку возможности любого математического пакета программ (MathCad, MathLab, Maple) ограничены, то решение (4.34) может оказаться не реализуемым. В этом случае предлагается второй способ к расчету дискретных передаточных функций компенсаторов. Анализ уравнения (4.33) показывает, что оно распадается на r подсистем, каждая из которых имеет вид:
W оu авт [ i ]· W кu авт [ i ]+ W оuu авт [ i ]= 0, i = 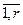. (4.35)
Очевидно, что каждое решение уравнения (4.33) порождает единственное решение всех подсистем вида (4.35) и наоборот каждая совокупность решений подсистем вида (4.35) образует одно решение уравнения (4.33).
Решение i -ой подсистемы (4.35) позволяет рассчитывать (r -1) компенсаторов, подключенных к выходу i -го регулятора, и как вытекает из (4.35), находится по формуле:
W кu авт [ i ]=-(W оu авт [ i ])-1· W оuu авт [ i ]. (4.36)
Зависимость (4.36) позволяет свести решение системы большой размерности (4.33) к последовательному решению r подсистем значительно меньшей размерности (в r раз). Благодаря этому становится возможным расчет дискретных передаточных функций компенсаторов из условия автономности для системы любого порядка с использованием выбранного математического пакета или системы программирования.
Рассмотрим пример, позволяющий уяснить реализацию полученного алгоритма расчета компенсаторов. Определим передаточные функции цифровых компенсаторов двумерной системы управления по формуле (4.34). Для этого запишем исходные матрицы:
|
|
|
W оu =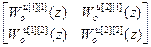 
, W кu = 
.
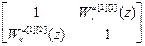Составим блочную матрицу W оu авт и блочные векторы W кu авт и W оuu авт.
W оu авт =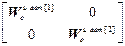 
.
Из матрицы W оu получаем:
W оu авт [1]=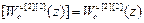 
,
W оu авт [2]= 
.
Отсюда: W оu авт =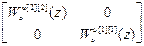 
,
W кu авт =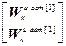 
.
Из матрицы W кu получим:
W кu авт [1]=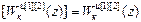 
,
W кu авт [2]=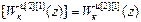 
.
Откуда: W кu авт =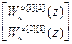 
,
W оuu авт =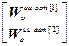 
.
Из матрицы W оu получим:
W оuu авт [1]=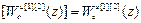 
,
W оuu авт [2]=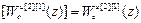 
.
Отсюда: W ouu авт =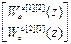 
.
Используя (4.34) получим первым способом передаточные функции компенсаторов:
W кu авт =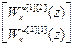 
=- 
=
=- 
=
= 
= 
.
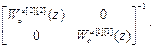
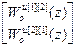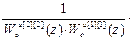
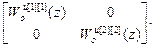
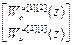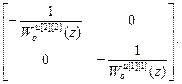
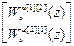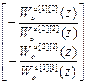Используя формулу (4.36), вторым способом получим:
W кu авт [1]= W кu [1][2](z)=-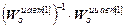 
=
=- 
,
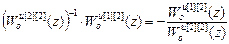W кu авт [2]= W кu [2][1](z)=-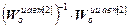 
=
=- 
.
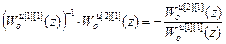Передаточные функции компенсаторов двумерной связанной ЦСУ, полученные двумя способами, удовлетворяют условию автономности [11], что подтверждает справедливость установленных зависимостей (4.34), (4.36).
Рассмотрим трехмерную систему управления и получим дискретные передаточные функции компенсаторов перекрестных связей по формуле (4.34).
W оu =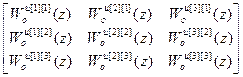 
,
W кu =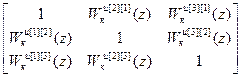 
.
Составим блочную матрицу W оu авт и блочные векторы W кu авт и W оuu авт:
W оu авт =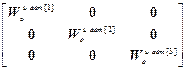 
,
W кu авт =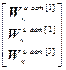 
, W оuu авт = 
.
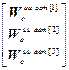Из матриц W оu и W кu получим матрицы W оu авт [ i ] и векторы W кu авт [ i ], W оuu авт [ i ], i =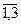 
:
W оu авт [1]=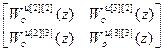 
,
W оu авт [2]=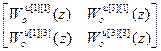 
,
W оu авт [3]=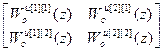 
,
W кu авт [1]=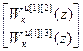 
, W кu авт [2]= 
,
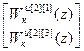W кu авт [3]=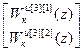 
,
W оuu авт [1]=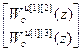 
, W оuu авт [2]= 
,
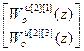W оuu авт [3]=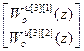 
.
После подстановки их в блочные W оu авт, W кu авт и W оuu авт, имеем:
W оu авт = =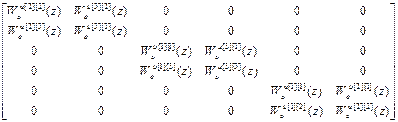 
,
W кu авт = 
, W оuu авт = 
.
В этом случае получим:
W кu авт =-(W оu авт)-1· W оuu авт =
=- 
.
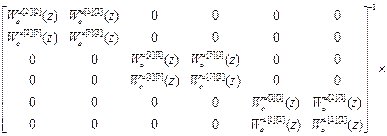
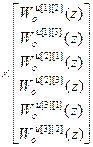Для расчета W кu авт по формуле (4.34) найдем обратную матрицу для трехмерной системы:
(W оu авт)-1=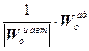 
,
где W оад – матрица, элементами которой являются алгебраические дополнения элементов матрицы W оu авт.
Вычислим определитель матрицы W оu авт:
| W оu авт |=
= Wоu [2][2](z)·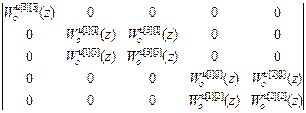 
–
– Wоu [3][2](z)·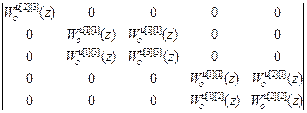 
=
= Wоu [2][2](z)· Wоu [3][3](z)·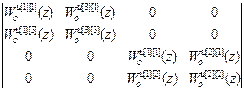 
–
– Wоu [3][2](z)· Wоu [2][3](z)· =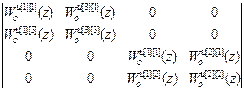
=(Wоu [2][2](z)· Wоu [3][3](z)– Wоu [3][2](z)· Wоu [2][3](z))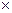
.
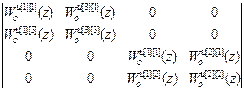Обозначим Δ1=(Wоu [2][2](z)· Wоu [3][3](z)– Wоu [3][2](z)· Wоu [2][3](z)), тогда:
| W оu авт |=Δ1· =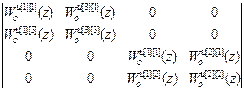
=
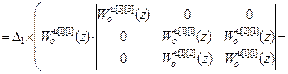
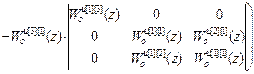=Δ1·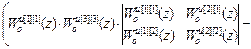 
=
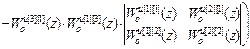=Δ1·(Wоu [1][1](z)· Wоu [3][3](z)– Wоu [3][1](z)· Wоu [1][3](z))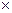
(Wоu [1][1](z)· Wоu [2][2](z)– Wоu [2][1]· Wоu [1][2])=Δ1·Δ2·Δ3,
где Δ2=(Wоu [1][1](z)· Wоu [3][3](z)– Wоu [3][1](z)· Wоu [1][3](z)),
|
|
|
Δ3=(Wоu [1][1](z)· Wоu [2][2](z)– Wоu [2][1](z)· Wоu [1][2](z)).
Таким образом | W оu авт |=Δ1·Δ2·Δ3.
Для получения матрицы W оад алгебраических дополнений транспонируем матрицу W оu авт :
(W оu авт ) Т =
= 
.
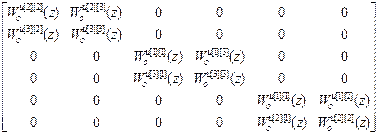Составим матрицу W оад алгебраических дополнений. У всех нулевых элементов матрицы (W оu авт ) Т алгебраические дополнения будут нулевыми:
W оад =
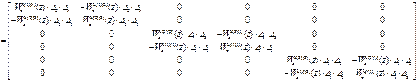Найдем обратную матрицу (W оu авт)-1:
(W оu авт)-1= =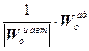 
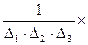
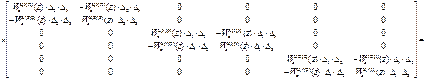
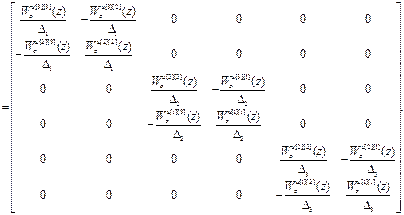
Получим передаточные функции компенсаторов по формуле (4.34):
W кu авт = =
.
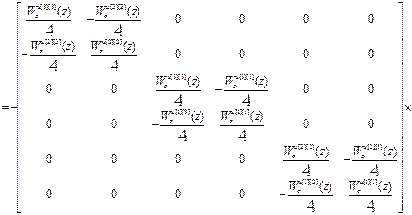
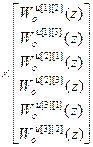Для компенсатора Wкu [1][2](z):
Wкu [1][2](z)=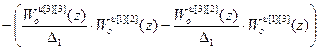 
=
= 
.
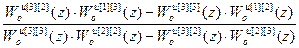Аналогично получаем передаточные функции остальных компенсаторов.
Отсюда:
.
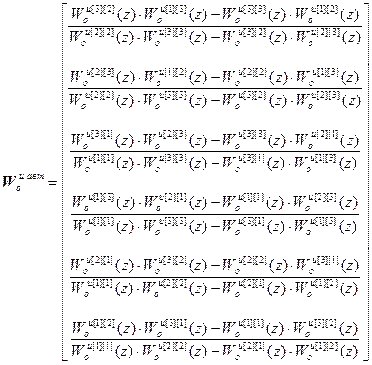Найдем передаточные функции компенсаторов, используя зависимость (4.36). Рассчитаем дискретные передаточные функции первой группы компенсаторов:
W кu авт [1]= –(W оu авт [1])-1· W оuu авт [1],
W кu авт [1]= =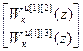
= – 
=
= – 
=
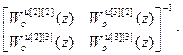
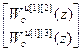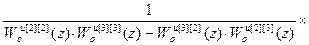
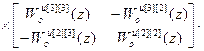
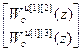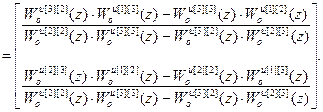
Для второй группы компенсаторов:
W кu авт [2]= –(W оu авт [2])-1· W оuu авт [2],
W кu авт [2]= =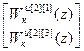
= – 
=
= – 
=
= 
.
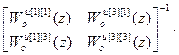
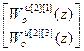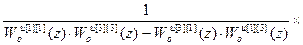
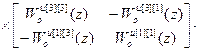
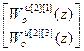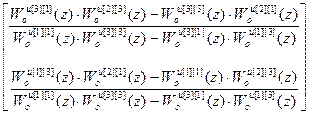Для третьей группы компенсаторов:
W кu авт [3]= –(W оu авт [3])-1· W оuu авт [3],
W кu авт [3]= =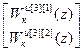
= – 
=
= – 
=
= 
.
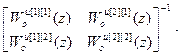
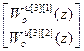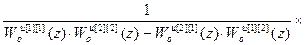
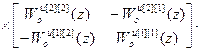
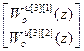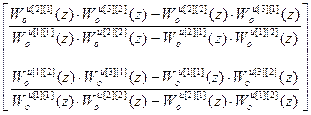Второй подход к диагонализации матрицы (W оu · W кu) заключается в решении векторно-матричного уравнения вида:
W оu · W кu = W ж, (4.37)
откуда передаточные функции компенсаторов перекрестных связей рассчитываются следующим образом:
W кu =(W оu)-1· W ж, (4.38)
где W ж – диагональная матрица желаемых передаточных функций.
В качестве примера, позволяющего уяснить реализацию полученного алгоритма расчета компенсаторов, определим передаточные функции цифровых компенсаторов двумерной системы управления. Для этого запишем исходные матрицы:
W оu =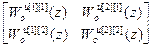 
, W ж = 
.
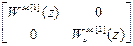Используя (4.38) получим передаточные функции компенсаторов:
W кu =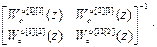 
=
= 
=
= 
=
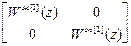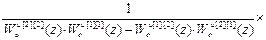
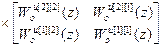
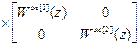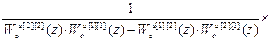
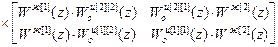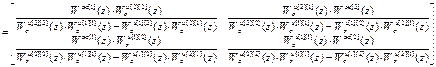
Отсюда:
W кu =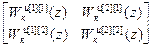 
.
Число компенсаторов для двумерной системы увеличилось на два по сравнению с первым подходом за счет введения компенсаторов прямой связи по основным каналам.
Рассмотрим трехмерную систему управления:
W оu = ,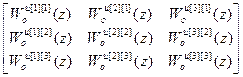
W ж =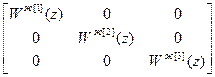 
.
Используя (4.38) получим передаточные функции компенсаторов:
W кu =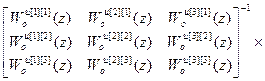 
.
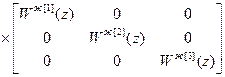Выполнив обращение и перемножив матрицы, получим следующие выражения для передаточных функций компенсаторов перекрёстных связей:
,
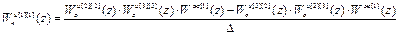
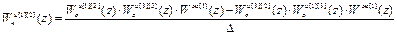
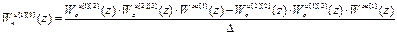
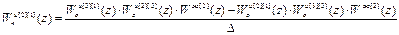
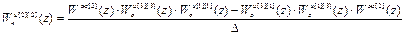
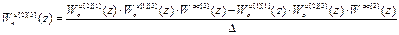
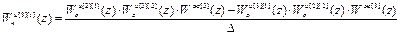
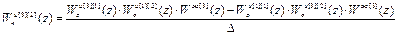
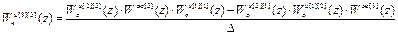где
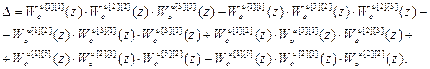W кu = 
.
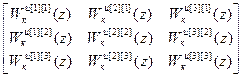Число компенсаторов увеличилось на три, то есть при втором подходе количество компенсаторов увеличивается на число равное размерности системы.
Анализ выражений (4.34), (4.36) и (4.38) и примеров расчета компенсаторов перекрестных связей позволяет указать достоинства и недостатки каждого из подходов.
Достоинством первого подхода по сравнению со вторым является:
1. Более простая структура передаточных функций (соответственно и разностных уравнений) компенсаторов перекрестных связей;
2. 
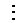
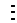
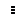
Меньшее число компенсаторов перекрестных связей. При использовании второго подхода их число увеличивается за счет введения компенсаторов по основным каналам, которые показаны на рис. 4.6 пунктирными линиями:
Рис. 4.6. Структурная схема системы связанного управления
r -мерным объектом (подход II)
Достоинством второго подхода по сравнению с первым является:
1. Возможность расчета таких компенсаторов перекрестных связей, которые обеспечивают требуемые динамические свойства системы управления, что определяется выбором W ж.
Использование зависимости (4.38) обеспечивает расчет компенсаторов перекрестных связей, при которых произведение W оu · W кu равно W ж. Тогда уравнение (4.29) примет вид:
y =(I + W ж · W рu)-1· W ж · W рu · y з. (4.39)
Отсюда:
= 
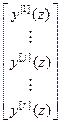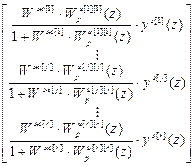. (4.40)
Из выражения (4.40) следует, что выбирая в качестве диагональных элементов матрицы W ж желаемые передаточные функции и оптимизируя по ним основные регуляторы, тем самым обеспечивается независимость управляемых величин друг от друга и требуемые динамические свойства системы по каналам: задающее воздействие – управляемая величина.
Отсюда получаем еще одно достоинство второго подхода:
2. Отсутствие необходимости расчета передаточных функций эквивалентных объектов для оптимизации настроек основных регуляторов (см. разд. 4.2.2).
Что же касается недостатков описанных подходов, то они противоположны достоинствам каждого из них.
