Расчет параметров основных цифровых регуляторов

Для анализа входов и выходов связанной системы управления перейдем от векторно-матричной формы (2.8) к скалярной:

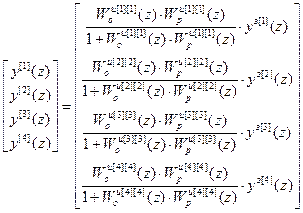. (2.11)

Анализ выражения (2.11) показывает, что 4-х мерную ЦСУ (рис. 2.2) при выполнении условия автономности можно представить эквивалентной схемой в виде совокупности четырех одномерных (одноконтурных) систем (рис. 2.4), каждая из которых включает соответствующий основной регулятор связанной системы (2.12) и эквивалентный объект с передаточной функцией (2.13):

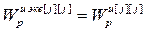, (2.12)

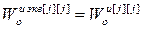, j = 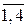. (2.13)

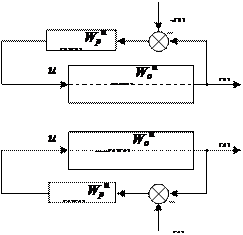
Рис. 2.4. Эквивалентная структурная схема АвЦСУ.

На основе полученных выражений (2.12)-(2.13) можно сделать следующие выводы:

1. Передаточные функции эквивалентных объектов многосвязного несимметричного ОУ (см. рис. 2.4) совпадают с передаточными функциями основных каналов (см. рис. 2.3).

2. Структура передаточных функций эквивалентных объектов не зависит от передаточных функций перекрестных каналов и передаточных функций компенсаторов перекрестных связей. Это в свою очередь приводит к значительному ускорению процедуры оптимизации параметров основных цифровых регуляторов, при этом улучшается сходимость оптимизируемого критерия к оптимуму.

Анализ (2.11) показывает, что в АвЦСУ каждая из управляемых величин 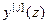является функцией только соответствующего задающего воздействия 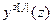и алгоритма управления 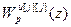. Следовательно, расчет параметров основных цифровых регуляторов управляющей части системы сводится к задаче скалярной оптимизации в одноконтурной системе на основе разностных уравнений соответствующих эквивалентных объектов.

Оптимизация параметров основных цифровых регуляторов может проводиться с использованием различных критериев. Наиболее часто для этих целей применяется квадратичная интегральная оценка, аналогом которой при построении дискретных систем управления является сумма квадратов ошибок управления:

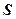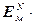
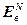= , (2.14)

где 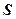=[ 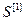,…, 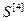] ^Т – вектор критериев каждой управляемой величины;

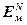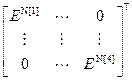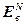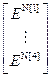= , = – блочная матрица и блочный вектор;

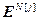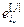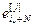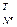=[ ,…, ] – вектор дискретных значений ошибок для j -ой управляемой величины; N^в = N +1 – объем выборки дискретных значений ошибок на период времени переходного процесса j -ой управляемой величины; 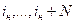– индексы такта квантования.

Условие экстремума примет вид:

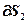=2· 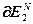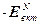= 0, (2.15)

где 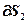= 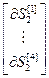– блочный вектор; 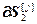=[ 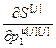,…, , 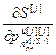,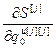…, 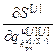] ^Т – вектор частных производных j -го критерия по всем настройкам j -го регулятора, 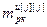; 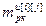= 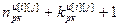– число переменных состояния разностного уравнения, описывающего динамические свойства регулятора, j = ;

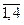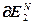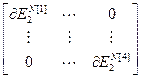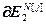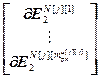= , = – блочная матрица и блочный вектор;

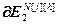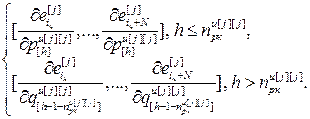= – матрица-строка значений частной производной j -ой ошибки управления по h -ой настройке j -го регулятора, N^в; j = 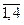, h = .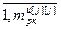

Поведение многомерной системы с учетом выражений (2.11)-(2.13) описывается следующей системой векторно-матричных уравнений:

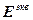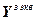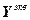= - , (2.16)

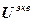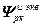
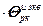= , (2.17)

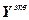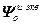
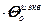= , (2.18)

где 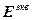– вектор ошибки управления; 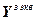– вектор заданий; 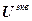=[ 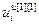,…, 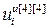] ^Т – вектор выходов регуляторов;

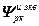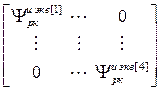= – блочная матрица; 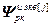– матрица-строка переменных состояния j -го регулятора; ;

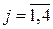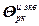– вектор настроечных параметров регуляторов; 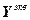– вектор управляемых величин;

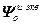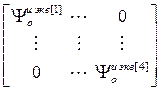= – блочная матрица;

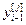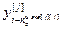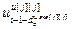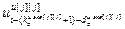=[ ,…, , ,…, ] – матрица-строка переменных состояния j -го эквивалентного ОУ, ; ;

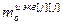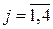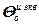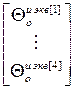= – блочный вектор; 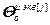=[ 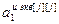,…, , 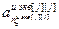,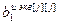…, 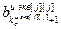] ^T – вектор параметров j -го эквивалентного ОУ, 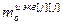; 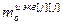= 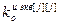+ +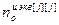1 – число переменных состояния эквивалентного ОУ; 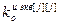, 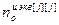– порядки числителя и знаменателя дискретной передаточной функции эквивалентного ОУ; 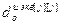– число тактов запаздывания эквивалентного ОУ; .

Расчет численных значений частных производных в векторно-матричной форме с учетом выражений (2.11)-(2.13):

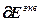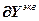=- , (2.19)

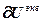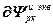
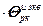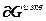= + , (2.20)

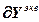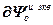
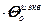= , (2.21)

где 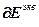– вектор частных производных всех ошибок управления по всем настройкам соответствующих регуляторов;

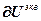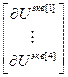= – блочный вектор; 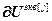=[ 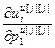,…, , 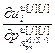,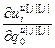…, 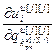] ^Т – вектор частных производных выхода j -го регулятора по всем его настройкам, ; ;

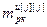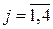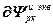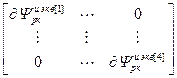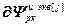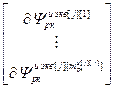= , = – блочная матрица и блочный вектор;

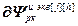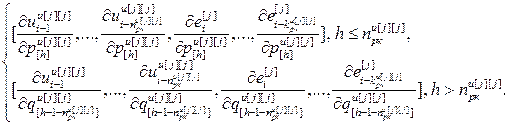= – матрица-строка частных производных переменных состояния j -го регулятора по его h -ой настройке, ; ;

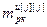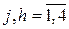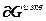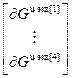= – блочный вектор; 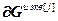=(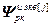) ^T – вектор переменных состояния j -го регулятора, используемых для расчета значений частных производных его выхода; ;

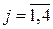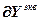– вектор частных производных выходов управляемых величин по всем настройкам соответствующих регуляторов;

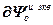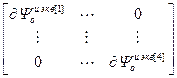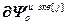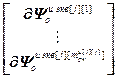= , = – блочная матрица и блочный вектор;

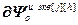= – матрица-строка частных производных переменных состояния j -го эквивалентного объекта управления по h -ой настройке j -го регулятора, ; .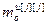

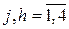После проведения первого этапа оптимизации, на котором в результате решения систем уравнений (2.16) – (2.21) вычисляются в начале векторы 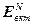и 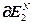, а затем значения вектора 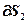(2.15), выполняется второй этап, на котором производится шаг по каждой настройке в направлении убывания критерия:

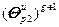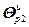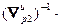
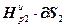=( – ) ^g, (2.22)

где g – номер итерации приближения к оптимуму; 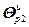= 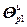– вектор настроечных параметров алгоритмов управления регуляторов;

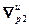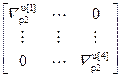= – блочная матрица; 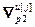= 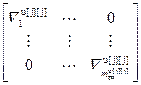– матрица нормы градиента j -го критерия, ;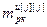

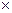
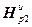– матрица коэффициентов шага; j = .

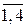Для вычисления коэффициента шага используются следующие выражения, записанные в матричной форме:

diag[(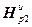) ^g ]=(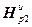) ^{g- 1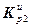}·() ^g, (2.23)

где 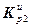– вектор переменных коэффициентов.

Значение j -го элемента вектора 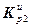определяется выражением:

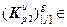
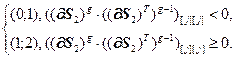(2.24)

Норма градиента вычисляется с помощью зависимости:

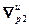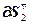=() ^Т ∙ 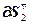, (2.25)

где 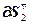= 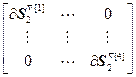, 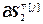= 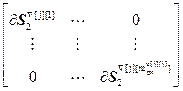– блочные матрицы;

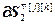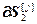= – вектор частных производных j -го критерия по всем настройкам j -го регулятора; j = 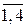, h = .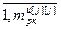

Момент окончания поиска оптимума определяется выполнением предварительно заданных условий:

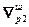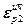< , (2.26)

или

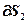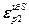< , (2.27)

где 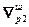=[ 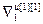,…, 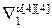] ^Т – вектор норм градиента всех критериев; 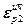=[ 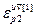,…, 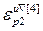] ^Т – вектор заданной точности расчета оптимальных значений настроек всех регуляторов при использовании условия (2.26);

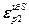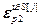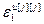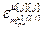= – блочный вектор; =[ ,…, ] ^Т – вектор заданной точности расчета оптимальных значений настроек j -го регулятора при использовании условия (2.27), 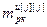; j = .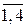

Для выполнения расчета выражений (2.16) – (2.18) и (2.19) – (2.21) необходимо предварительно задаться начальными условиями:

, , , ,

, ,

,

,

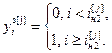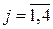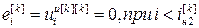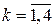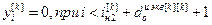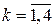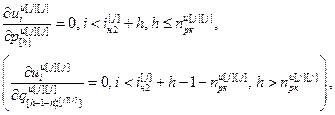
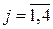
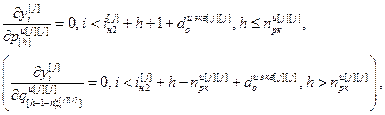
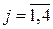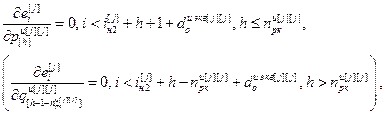
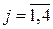где i_{н 2}^{[ j ]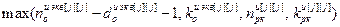}= – значение номера такта, с которого начинается расчет переходного процесса .

Таким образом, предложен алгоритм оптимизации параметров основных цифровых регуляторов в составе АвЦСУ. Преимуществом данного алгоритма является возможность использования значительно менее мощных средств ЦВТ с относительно небольшими объемами оперативной памяти, при этом реализация рассмотренного алгоритма может проводиться как с использованием широко известных языков программирования (C++, Pascal, Fortran), так и с помощью вычислительных математических пакетов (MathCAD, Matlab, Maple).

2.2.4. Расчет инвариантных компенсаторов возмущений

Следующим этапом расчета управляющей части системы является расчет компенсаторов возмущений из условия инвариантности.

Из соотношения (2.7) получим выражение для расчета передаточных функций компенсаторов возмущений, удовлетворяющих условию инвариантности:

W _к^f =(W _к^u)^-1·(W _о^u)^-1·(- W _o^f). (2.28)

Выражая из (2.9) (W _о^u)^-1:

(W _о^u)^-1= W _к^u · W _р^u · R ^-1, (2.29)

можно записать эквивалентную формулу расчета передаточных функций компенсаторов возмущений:

W _к^f =(W _к^u)^-1· W _к^u · W _р^u · R ^-1·(- W _o^f),

W _к^f = W _р^u · R ^-1·(- W _o^f). (2.30)

Поскольку при выполнении условия автономности R является диагональной матрицей, то из (2.30) получим формулу расчета передаточных функций инвариантных компенсаторов возмущений:

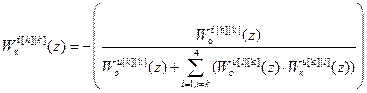. (2.31)

Используя (2.31) получим передаточные функции компенсаторов возмущений.

;

;

;

;

;

;

;

;

;

;

;

.

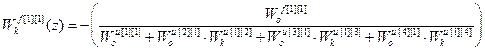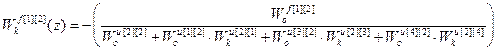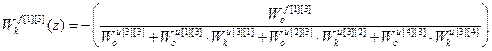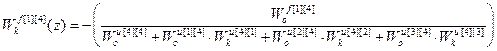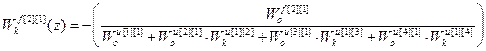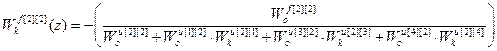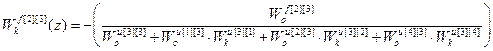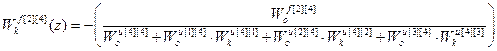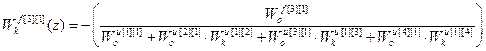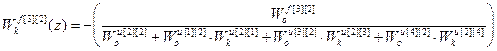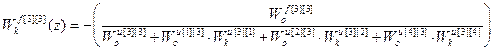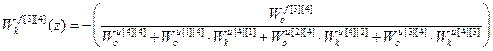С учетом структуры матрицы дискретных передаточных функций объекта по каналам управления W _о^u и возмущения W _о^f, а так же матрицы дискретных передаточных функций компенсаторов перекрестных связей W _к^u получаем:

; ; ;

; ; ;

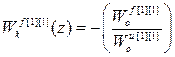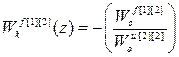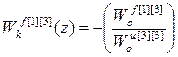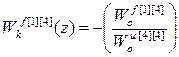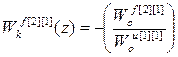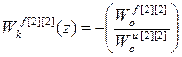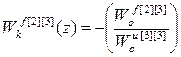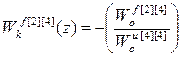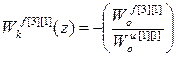; ; ; (2.32)

; ; .

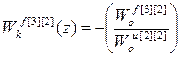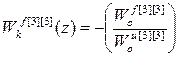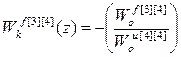Анализ передаточных функций компенсаторов возмущений (2.32) позволяет сделать следующие выводы:

1. Структура передаточных функций компенсаторов возмущений многосвязного несимметричного объекта имеет достаточно простую структуру.

2. Динамика компенсаторов возмущений не зависит от передаточных функций перекрестных каналов многосвязного объекта и компенсаторов перекрестных связей.

Таким образом, для несимметричного многосвязного объекта – процесса синтеза аммиака – разработана структура цифровой связно-комбинированной системы управления, выведены формулы для расчета компенсаторов перекрестных связей из условия автономности и компенсаторов возмущений из условия инвариантности, получены передаточные функции эквивалентных объектов и предложен алгоритм оптимизации параметров основных цифровых регуляторов по среднеквадратичному критерию качества. Кроме того, поскольку передаточные функций компенсаторов возмущений не зависят от динамики передаточных функций компенсаторов перекрестных связей и передаточных функций перекрестных каналов, то для несимметричных ОУ 2 и 3 этапы расчета управляющей части системы (п. 2.2.1) алгоритма можно выполнять независимо друг от друга, а при достаточных возможностях средств цифровой вычислительной техники – одновременно.