Геометрично незмінні системи (споруди) - це системи які задовольняють слід. вимогу споруда повинна зберігати додану йому геометричну форму протягом всього терміну служби.
Геометрично незмінною називається система, не змінює додану їй геометричну форму ні за яких змінах положення її в просторі.
Змінна система -яка здатна змінювати свою геометричну форму без деформації матеріалу за рахунок кінцевих переміщень її елементів як твердих тіл.
Ступінь свободи і ступінь незмінності системи.
Ступені свободи - це сукупність незалежних координат переміщення і / або обертання, повністю визначає рух і / або положення тіла або системи тіл.
Наприклад
Тверде тіло, що рухається в тривимірному просторі, максимально може мати шість ступенів свободи: три поступальних і три обертальних.
• Автомобіль, якщо його розглядати як тверде тіло, переміщається по площині, а точніше кажучи, за деякою двовимірної поверхні (в двовимірному просторі). Він має три ступені свободи (одну обертальну, і дві поступальні).
• Поїзд змушений переміщатися по рейковому шляху, і тому він має тільки одну ступінь свободи.
Свобода системи - це її можливість здійснювати будь-які рухи щодо землі без деформації матеріалу.
Питання для самоперевірки:
1. Що вивчає статика споруд?
2. Гіпотези та припущення статики споруд
3. Поняття розрахункової схеми.
4. Класифікація споруд.
5. Назвіть опорні пристрої.
6. Які види навантажень?
7. Що таке геометрично змінні і незмінні системи?
8. Що називають ступіню свободи і ступіню незмінності системи?
Питання для самостійного вивчення:
1. Класифікація споруд. Опорні пристрої. Види навантажень.
2. Миттєво змінні системи.
3. Необхідна умова геометричної незмінності системи.
Література:
1. Мухин Н.В., Першин А.Н., Шишман Б.А. «Статика сооружений», - М. «Высшая школа», 1980 с.5-40, с.114-145
2. Сетков В.И. Сборник задач для расчетно-графических работ по технической механике. М.: 1989 с.
ЛЕКЦІЯ № 13
Тема 3.3. Статично визначувані плоскі ферми
План лекції
1. Статично визначувані плоскі ферми
2. Визначення зусиль у стержнях ферми аналітичним способом
С/Р 3. Поняття про статично визначені та статично невизначені системи.
1 Статично визначувані плоскі ферми
Рамні системи мають широке застосування в залізобетонних і
металевих конструкціях. Рідше вони застосовуються в дерев'яних конструкціях,
Встановивши статичну визначність рами, підтверджуємо, що виконано і необхідна умова її геометричної незмінюваності ЯКЕ??????
Не змінювати надану їй геометричну форму ні за яких змінах
однак щоб остаточно переконатися в незмінності рами, треба провести її структурний аналіз РОЗРАХУНОК - ВИЗНАЧИТИ ЗУСИЛЛЯ У КОЖНОМУ окремі елементи конструкції.
На прикладі ферми, ми навчимося визначати зусилля в кожному окремому елементі і конструкції в цілому і доведемо, що наша конструкція задовольняє всім вимогам, тобто міцною, стійкою, ЖОРСТКОЮ, економічною!
Згадаймо!!!
Умова рівноваги: 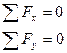
Проекції сил на осі:
Визначення кутів:
Синус кута х - це відношення протилежного катета до гіпотенузи: sinx = а/с
Косинус кута х -це відношення прилеглого катета до гіпотенузи сosx= в/с
Тангенс кута х - це відношення протилежного катета до прилеглому: tgx = а/в
Котангенс кута х - це відношення прилеглого катета до протилежного:
ctgx = в/а
Порядок обчислення такий:
1. На схемі ферми всі вузли позначають буквами, а всі стрижні - цифрами.
2. По черзі вирізують всі вузли ферми і викреслюють їх силові схеми, позначаючи стрілками зусилля в перерізаних стержнях і зовнішні сили, прикладені до даного вузла. Зусилля зображують напрямками від вузла, тобто вважають, що всі стержні розтягнуті.
3. У центр кожного вузла поміщають початок осей координат, складають рівняння рівноваги для сходяться у вузлі сил і знаходять невідомі зусилля. Якщо при обчисленні зусилля вийде з негативним знаком, значить воно спрямоване в протилежну сторону, тобто не від вузла, а до вузла і, отже, відповідний
стрижень не розтягнутий, а стиснут. Якщо дорівнює «0» - значить стрижень не працює.
Порядок вирізання вузлів повинен бути таким, щоб у кожен послідовно розглянутий вузол входили тільки два стержня, зусилля в яких невідомі.
Так, переходячи від вузла до вузла, знайдемо зусилля в усіх стержнях ферми.
2. Визначення зусиль у стержнях ферми аналітичним способом
Аналітичний спосіб рішення:
2. Накреслити задану схему. Позначити стрижні - цифрами– цифрами
1,2,3, вузли –буквами А,Б,В.
По черзі викреслювати кожен вузол!
3. Вибрати об’єкт рівноваги - першу точку А, в якій максимум
відомих сил. До об’єкту додати всі відомі сили, які зійшлись в т.А
замініті зв'язку зусиллями S1, позначаючи стрілкамі від точки (припускаючи, що стрижень розтягнутий)
4. Вибрати осі координат. Зручну задати так, щоб вісь проходила
перпендикулярно лінії дії хоча б одній з невідомих сил, тобто невідомих має бути не більше двух.
5. Спроектувати всі сили та реакції на вибрані осі – скласти рівняння рівноваги з умови 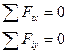
6. З рівнянь визначаємо невідомі необхідні ЗУСИЛЛЯ.
(Якщо S= 0, то стержень не працює; S= (-), стержень стислий, реакція спрямована до вузла; S= (+), стержень розтянут, реакція спрямована від вузла,)
Порядок вирізання вузлів повинен бути таким, щоб у кожен послідовно розглянутий вузол входили тільки два стержня, зусилля в яких невідомі.
Так, переходячи від вузла до вузла, знайдемо зусилля в усіх стержнях ферми.
Приклад № 3 Визначити зусилля в стержнях 1,2,3,4 ферми
Аналітичний спосіб рішення:
Викреслюємо задану схему(обов’язково в прийнятому масштабі). Позначаємо стержні цифрами, вузли буквами. На схемі вказуємо всі відомі значення – розміри висоти, довжини, значення сил
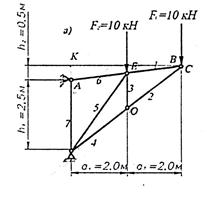
1. Визначення зусиль в стержнях ферми виконуємо поступовим
вирізуванням вузлів. Розглядаємо вузли як систему збіжних сил, використовуючи рівняння рівноваги. Першим треба взяти вузол, в якому збіжними є мінімум два стержня.
Для визначення зусиль в стержнях 1 і 2 вирізаємо вузол С.
2. Викреслюємо розрахункову схему для першого вузла (рис 2):
a. Вибираємо об’єкт рівноваги - вузол С.
b. до об’єкту додати всі відомі сили, які зійшлись в т. С, вказуємо на схемі кути.
c. від об’єкту подумки відкинути зв’язки і замінити їх реакціями R1 і R2 (реакція позначається як номер стержня)
Вибираємо осі координат.
 2015-03-20
2015-03-20 4912
4912
