Ортогонализация Шмидта

В общем случае система линейно независимых функций 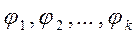не является ортонормальной.

Всякую линейную независимую систему функций 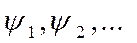заданную в действительном линейном пространстве со скалярным произведением можно ортогонализировать к системе 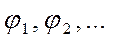, так что 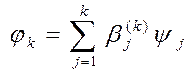, где 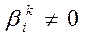- действительные числа.

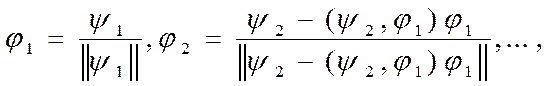
(27)

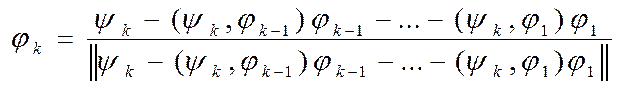
Пример:

Так, система степеней 1, x, x² … (степенной ряд) в пространстве L₂(-1,1) может быть ортогонализирована к системе нормированных полиномов Лежандра (домашнее задание).

В (1) 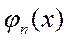- система ортогональных функций. Если в качестве этой системы взять систему тригонометрических 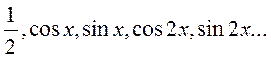функций, то они образуют ортогональную систему функций в пространстве L₂(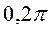) с интегрируемым квадратом модуля на .

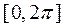Ряды Фурье по этой конкретной системе будут сейчас рассмотрены.