Рассмотрим периодическую функцию 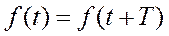
При выполнении ряда условий (кусочность, гладкость, ограниченность) она раскладывается в тригонометрический ряд или ряд Фурье
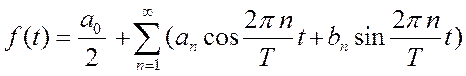 (28)
(28)
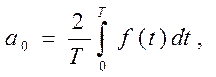
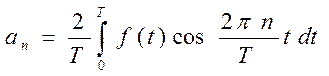
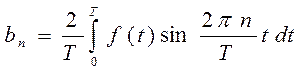 (29)
(29)
где 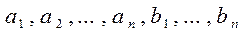 - коэффициенты ряда Фурье.
- коэффициенты ряда Фурье.
Действительно, если умножить (28) на 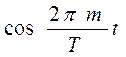 и проинтегрировать, то:
и проинтегрировать, то:
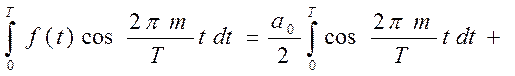
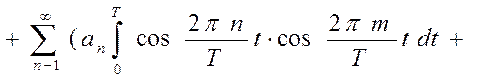
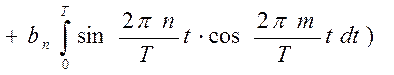
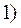
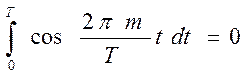
 |
Очевидно, что
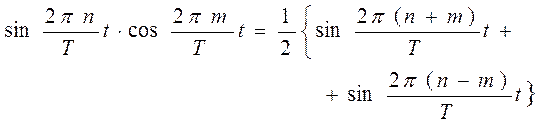
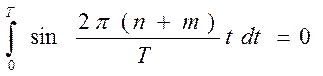 тогда
тогда
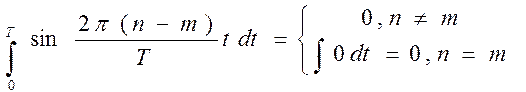
2)
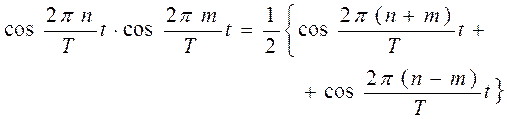
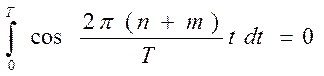
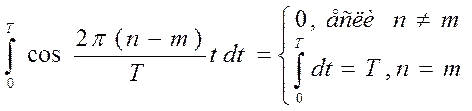
Тогда, остаётся
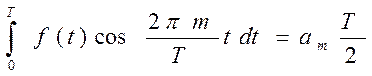
Откуда и следует определение 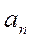 (см.(29)). Аналогично
(см.(29)). Аналогично 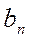 . (Домашнее задание).
. (Домашнее задание).
Если функции 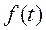 задана только на отрезке [0,T], то её всегда можно сделать периодической.
задана только на отрезке [0,T], то её всегда можно сделать периодической.
 |
f(t)






 |  |  | |||
 |  |  | |||
 |  |  |
 0 T 2T 3T t
0 T 2T 3T t
Такой сигнал нельзя спутать с сигналом,
 |
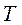
 |  |
где на краях всегда нули (это означает, что приёмник всегда включён). Такой сигнал уже никогда не сделать периодическим.
На практике, приёмник всегда имеет время включения и время выключения, поэтому всегда в качестве периода можно взять время работы приёмника.
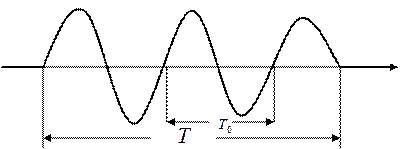 |
Сигнал периодичен с T, но в тоже время в нём видна периодичность с T 0. С такими сигналами мы встретимся дальше.
Чётная функция 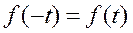
Тогда 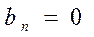 и ряд раскладывается только по косинусам.
и ряд раскладывается только по косинусам.
Нечётная функция 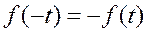
Тогда 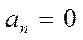 и ряд только по синусам.
и ряд только по синусам.
Бывает «сдвинутая» чётность, когда 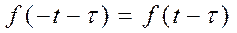
с этими случаями также встретится позже.
Любая функции может быть представлена в виде суммы чётной и нечётной функций.
Введём
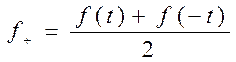
Очевидно её чётность 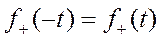
Введём 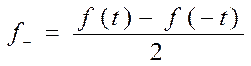
Она нечётна 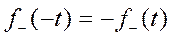
Но тогда 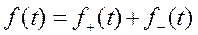
При этом, формулы для четной и нечетной функции будут иметь вид:
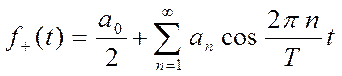 (30)
(30)
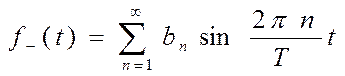
 2015-03-07
2015-03-07 272
272








