Эквивалентность автоматов

Эквивалентность автоматов определяют по их одинаковой реакции на входные последовательности символов, то есть по формированию одинаковых выходных последовательностей символов.

Так как модель автомата представляет трехосновную алгебру, то для сравнения двух автоматов необходимо найти три оператора, формирующих отображение множеств X, Q и Y модели одного автомата на соответствующие множества модели другого автомата. После этого необходимо оценить влияние этих операторов на исполнение функций переходов и выходов каждым автоматом. Если на одинаковые последовательности входных символов автоматы генерируют одинаковые последовательности выходных символов, то такие автоматы эквивалентны.

Рассмотрим модели двух абстрактных автоматов:

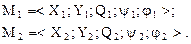(1.23)

Пусть даны операторы:

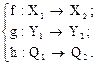(1.24)

Если при исполнении функций переходов и выходов выполняются условия:

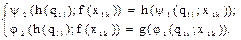(1.25)

то совокупность операторов q=(f;g;h) формирует гомоморфное отображение модели автомата М₁ на модель автомата М₂ когда каждому значению x_1kÎX₁, y_1jÎY₁ и q_1iÎQ₁ соответствуют единственные образы x_2kÎX₂, y_2jÎY₂, q_2iÎQ₁.

Пусть даны операторы:

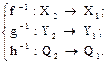(1.26)

Если при исполнении функций переходов и выходов выполняются условия:

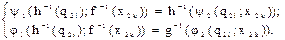(1.27)

то совокупность операторов q^-1 = áf^-1;g^-1;h^-1ñ определяет гомоморфное отображение модели автомата М₂ на модель автомата М₁ когда каждому значению x_2kÎX₂, y_2jÎY и q_2iÎQ₂ соответствуют единственные образы x_1kÎX₁, y_1jÎY₁, q_1iÎQ₁ .

Если найдена совокупность операторов (q;q^-1), для которой

q_°q^-1= q^-1_°q =1, (1.28)

то такое взаимное отображение называют изоморфным.

Изоморфное отображение рефлексивно, симметрично и транзитивно. Особый интерес для оценки эквивалентности автоматов представляет случай, когда f=1. По условиям (1.25) и (1.27) для x_kÎX имеем:

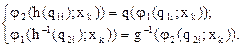(1.29)

Если существуют такие q_1i и q_2i, для которых значения функций выходов j₁(q_1i;x_k) и j₂₍q_2i;x_k) совпадают для всех x_kÎX, то есть

j₁(q_1i;x_k)=j₂(q_2i;x_k), (1.30)

то g=g^-1=1, h(q_1i)=q_2i, h^-1(q_2i)=q_1i. При этом Y₁=Y ₂ =Y. Такие состояния q_1i и q_2i называют неотличимыми по выходам автоматов.

В результате просмотра множества пар неотличимых состояний (q_1i;q_2i)Î(Q₁ÄQ₂) можно найти несколько подмножеств, которые формируют разбиение множества (Q₁ÄQ₂) на классы неотличимых по выходу состояний.

Если для пары неотличимых состояний (q_1i;q_2i) значения функций переходов формируют для всех символов x_kÎX также пары неотличимых состояний (y(q_1i[t];x_k[t]);y(q_2i[t];x_k[t])), то состояния q_1i и q_2i называют совместимыми. В результате такого просмотра всех пар одного класса неотличимых состояний формируется его разбиение на классы совместимых состояний.

Состояния q_1i и q_2i являются эквивалентными, если для всякой входной последовательности a=(x₁x₂...x_n) выполняется условие:

М₁(q_1i;a)=М₂(q_2i;a), (1.31)

Поэтому необходимо проследить изменения значений функций переходов (y(q_1i[t];x_k[t]);y(q_2i[t];x_k[t])) для каждого символа входной последовательности a=(x₁x₂...x_n).

Множество всех пар (q_1i;q_2i), для которых выполняется условие (1.31), формирует класс эквивалентных состояний.

Если входной и выходной алфавиты у двух автоматов совпадают, то автомат M₂ покрывает автомат M₁, если j₂(h(q_1i);a)=j₁(q_1i;a) для всех aÎXⁿ, а автомат M₁ покрывает автомат M₂, если входной и выходной алфавиты у этих автоматов общие и
j₁(h^-1(q_2i);a)=j₂(q_2i;a) для всех aÎXⁿ.

По условиям изоморфизма автоматы M₁ и M₂ эквивалентны, если M₁ покрывает M₂ и M₂ покрывает M₁. У эквивалентных автоматов существуют эквивалентные состояния q_1i и q_2i.

Если для эквивалентных автоматов М₁ и М₂ имеем ÷Q₁÷ < ÷Q₂÷, то автомат М₁, имеющий меньшее число состояний m₁ = ÷Q₁÷, покрывает автомат М₂, имеющий большее число состояний m₂ = ÷Q₂÷. Автомат, который нельзя покрыть автоматом с меньшим числом состояний, называют минимальным.

Для поиска эквивалентных состояний q_1i и q_2i удобно использовать таблицы переходов пар состояний двух автоматов. В каждой паре левый элемент есть состояние автомата М₁, а правый элемент - состояние автомата М₂. Левый столбец такой таблицы предназначен для указания неотличимых пар состояний, которые формируются по таблицам выходов автоматов следующим правилом:

"если среди множества состояний двух автоматов Q₁ и Q₂ найдется такая пара (q₁;q₂), у которой значения функций выходов равны для каждого символа входного алфавита x_kÎX, т.е. j₁(q_1i;x_k)=j₂(q_2i;x_k), то состояния q₁ и q₂ неотличимы;"

Позициями таблицы являются пары состояний двух автоматов, в которые они переходят из соответствующих состояний пары неотличимых состояний при подаче на входы автоматов символа x_k. Значения очередных состояний могут быть найдены по таблицам переходов автоматов М₁ и М₂ для соответствующего символа x_kÎX, т.е. (q₁=y(q_1i;x_k); q₂ = y(q_2i;x_k)).

Пусть таблица переходов пар состояний двух автоматов представлена таблицей 1.19, где пары неотличимых состояний, приведенные в левом столбце, есть (q_1i;q_2j), (q_1j;q_2p), (q_1p;q_2s), (q_s;q_2i).

текущая пара неотличимых состояний (q1;q2)	символы входного алфавита xiÎX
x1	x2	…	xn
…	…	…	…	…
(q1i;q2j)	(q1i;q2j)	(q1j;q2p)	…	(q1s;q2i)
(q1j;q2p)	(q1i;q2j)	(q1p;q2p)	…	(q1s;q2i)
(q1p;q2s)	(q1j;q2p)	(q1j;q2p)	…	(q1j;q2p)
(q1s;q2i)	(q1s;q2p)	(q1p;q2j)	…	(q1j;q2i)
…	…	…	…	…

Анализ таблицы показывает, что

1) состояния q_1i и q_2j совместимы, т.к. при приеме каждого символа входного алфавита неотличимые состояния автоматов М₁ и М₂ переходят в в пары также неотличимых состояний;

2) состояния q_1p и q_2s совместимы, т.к. при приеме каждого символа входного алфавита неотличимые состояния автоматов М₁ и М₂ остаются в одной паре неотличимых состояний;

3) состояния q_1j и q_2p несовместимы, т.к. при приеме символа x₂ неотличимые состояния автоматов М₁ и М₂ переходят в различные пары неотличимых состояний;

4) состояния q_1s и q_2i несовместимы, т.к. при приеме каждого символа входного алфавита неотличимые состояния автоматов М₁ и М₂ переходят в различные пары неотличимых состояний.

Следовательно, автоматы М₁ и М₂, даже при наличии совместимых состояний, не эквивалентны между собой.

Пример 1.5. Пусть даны автомат M₁=áX₁;Y₁;Q₁;y₁;j₁ñ, где X₁={0;1}, Y₁={0;1}, Q₁={q₁₁;q₁₂;q₁₃}, y₁ и j₁ (см. таблицу 1.20) и автомат M₂=áX₂;Y₂;Q₂;y₂;j₂ñ, где X₂={0;1}, Y₂={0;1}, Q₂={q₂₁;q₂₂}, y₂ и j₂ (см. таблицу 1.21).

Граф автомата М₁ приведен на рис.1.13, автомата М₂ - на рис.1.14. Определить эквивалентность автоматов М₁ и М₂.

текущее состояние qÎQ1	символы входного алфавита xÎX1		текущее состояние qÎQ2	символы входного алфавита xÎX2
q11	q13;0	q12;1		q21	q21;0	q22;1
q12	q11;1	q13;0		q22	q21;1	q21;0
q13	q11;0	q12;1

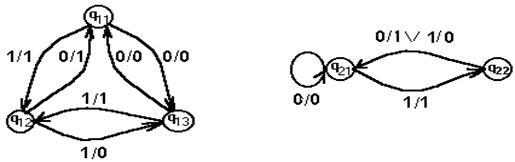
Рис.1.13 Граф автомата М₁ Рис.1.14 Граф автомата М₂

Для автоматов М₁ и М₂ неотличимыми по выходу являются пары состояний (q₁₁;q₂₁), (q₁₂;q₂₂) и (q₁₃;q₂₁). При этом формируются два класса неотличимых состояний {(q₁₁;q₂₁);(q_13;q₂₁)} и {(q₁₂;q₂₂)}.

Если для неотличимой пары (q₁₁;q₂₁) при входном символе "0" автоматы М₁ и М₂ переходят в неотличимую пару состояний (q₁₃;q₂₁), а при входном символе "1" - в неотличимую пару (q₁₂;q₂₂), то состояние q₁₁ автомата М₁ и состояние q₂₁ автомата М₂ являются совместимыми.

Если для неотличимой пары состояний (q₁₂;q₂₂) при входном символе "0" автоматы М₁ и М₂ переходят в неотличимую пару состояний (q₁₁;q₂₁), а при входном символе "1" - в неотличимую пару (q₁₃;q₂₁), то состояние q₁₂ автомата М₁ и состояние q₂₂ автомата М₂ также являются совместимыми.

И наконец, если для неотличимой пары состояний (q₁₃;q₂₁) при входном символе "0" автоматы М₁ и М₂ переходят в неотличимую пару состояний (q₁₁;q₂₁), а при входном символе "1" - в неотличимую пару (q₁₂;q₂₂), то состояние q₁₃ автомата М₁ и состояние q₂₁ автомата М₂ являются совместимыми.

Если состояние q₁₃ автомата М₁ совместимо с состоянием q₂₁ автомата М₂, а состояние q₂₁ автомата М₂ совместимо с состоянием q₁₁ автомата М₁, то согласно свойству транзитивности состояние q₁₁ автомата М₁ совместимо с состоянием q₁₃ автомата М₁.

Проверку эквивалентности автоматов можно выполнить, обрабатывая одинаковые последовательности символов каждым автоматом и анализируя последовательности символов на их выходах.

Пусть для автомата М1 имеем q₁₁=q₀ и a = (01010101). Тогда процесс обработки входного слова формирует следующие последовательности:

вход: 0[1] 1[2] 0[3] 1[4] 0[5] 1[6] 0[7] 1[8];

q: q₁₁[1] q₁₃[2] q₁₂[3] q₁₁[4] q₁₂[5] q₁₁[6] q₁₂[7] q₁₃[8] q₁₂[9];

выход: 0[1] 1[2] 1[3] 1[4] 1[5] 1[6] 1[7] 1[8],

то есть b₁= (01111111).

Пусть для автомата М₂ имеем q₂₁=q₀ и a=(01010101). Тогда процесс обработки входного слова формирует следующие последовательности:

вход: 0[1] 1[2] 0[3] 1[4] 0[5] 1[6] 0[7] 1[8];

q: q₂₁[1] q₂₁[2] q₂₂[3] q₂₁[4] q₂₂[5] q₂₁[6] q₂₂[7] q₂₁[8] q₂₂[9];

выход: 0[1] 1[2] 1[3] 1[4] 1[5] 1[6] 1[7] 1[8],

то есть b₂= (01111111).

Итак, автоматы М₁ и М₂ эквивалентны. Так как автомат М₂ имеет меньшее число внутренних состояний, то он покрывает автомат М₁.