Минимальный автомат - это автомат, имеющий наименьшее возможное количество состояний и реализующий заданную функцию выходов.
Два состояния автомата называются 1-эквивалентными, если, находясь в любом из этих состояний, автомат на один и тот же входной сигнал (входное слово длиной в 1) выдает один и тот же выходной сигнал. Два состояния автомата называются К- эквивалентными, если, начиная с любого из этих состояний, автомат на любые одинаковые слова длины К выдает одинаковые выходные слова (также длины К). Если два состояния К- эквивалентны для любых К, то их называют (просто) эквивалентными. Множество попарно эквивалентных состояний образует класс эквивалентности.
Смысл минимизации состоит в выявлении классов эквивалентности и замене каждого класса одним состоянием. Процедура минимизации состоит в следующем:
1. По таблице выходов автомата Мили (или по первой строке отмеченной таблице переходов автомата Мура) находятся состояния, имеющие одинаковые столбцы (отмеченные одинаковыми выходными сигналами) – это 1-эквивалентные состояния.
2. Далее используется таблица переходов. Все состояния, входящие в 1-эквивалентный класс, которые под воздействием первого сигнала перешли в состояния, принадлежащие в свою очередь 1-эквивалентному классу, образуют 2-эквивалентный касс.
3. Процедура разбиения на классы эквивалентности продолжается до тех пор, пока при очередном шаге К- эквивалентные классы не совпадут с (К-1)-эквивалентными, т.е. получатся эквивалентные классы.
4. Все состояния, входящие в один класс эквивалентности, заменяются одним состоянием.
Пример. Рассмотрим автомат Мили
| X1 | Y1 | Y1 | Y1 | Y1 | Y1 | Y2 |
| X2 |  Y2 Y2 | Y2 | Y2 | Y2 | Y2 | Y2 |
|
|
| X1 | ||||||||||||
| α | α | β | α | β | α | |||||||
| X2 | ||||||||||||
| α | α | α | α | α | α |
|
|
|
|
|
1 – эквивалентные классы определяются из табл. 8, 2 – эквивалентные из табл. 9, а 3 – эквивалентные и просто эквивалентные из табл. 10.
Таблица 10
| X1 | ||||||||||||
| α | α | α | γ | γ | α | |||||||
| X2 | ||||||||||||
| α | α | α | β | β | β |
В качестве имен состояний минимального автомата возьмем имена классов. Минимальный автомат представлен табл. 11 и 12. Таблица 11 Таблица 12
| α | β | γ | α | β | γ | |||
| X1 | α | γ | α | X1 | Y1 | Y1 | Y2 | |
| X2 | α | β | β | X2 | Y2 | Y2 | Y2 |
РАСПОЗНАЮЩИЕ АВТОМАТЫ
Распознающий автомат – это автомат Мура, в котором фиксируется начальное состояние и подмножество состояний F⊂Q, называемое множеством заключительных состояний. Говорят, что автомат допускает (принимает, распознает, представляет) данное слово, если реакцией на это слово может быть переход автомата в одно из заключительных состояний.
Примеры. 1. Автомат (рис. 4) с начальным состоянием 1 и заключительным F1 и F2 допускает слова, в которых имеются только парные вхождения букв a и b, например,
a a, a a a a a a, b b a a и т.д.
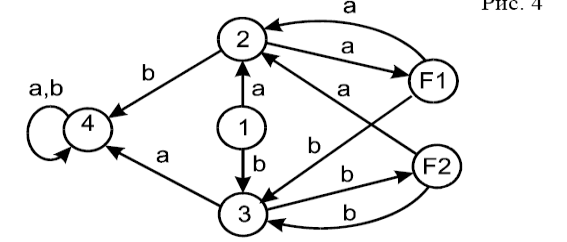
Для распознавания часто используются частичные автоматы (рис.5), допускающие тоже множество слов, что и автомат, показанный на рис.4.
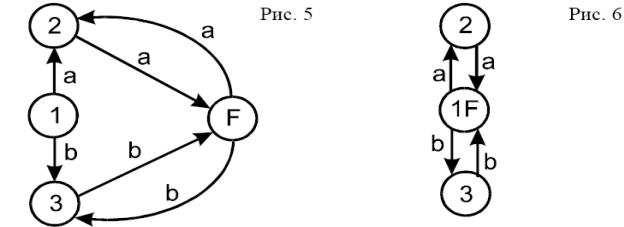
Здесь начальное состояние 1, а заключительное F. Слово считается недопустимым, если в результате реакции на него автомат не остановится в заключительном состоянии или если будет подан запрещенный (для данного состояния) входной сигнал. Например, воздействие входного слова ab на автомат вызовет переход в состояние 2 по букве a, но в этом состоянии не определен переход по букве b, следовательно, слово ab недопустимо. Если считать пустое (не содержащее ни одной буквы) слово допустимым, то можно еще более упростить частичный автомат, объединив начальное и заключительное состояния (рис.6).
3.Одним из наиболее широко используемых на практике типов распознающих автоматов является частичный недетерминированный автомат. Недетерминизм проявляется в том, что из одного состояния по одному и тому же входному сигналу возможны переходы в различные состояния, т.е. функция переходов заменяется отношением переходов. Недетерминированный автомат (рис.7) принимает, например, слова ab, aa, bb, bba и т.д. здесь начальное состояние A, а заключительное -F.
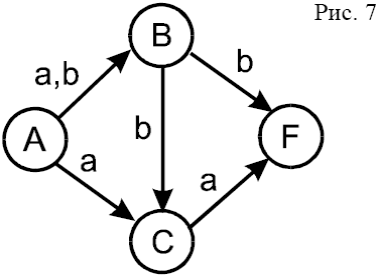
Таблица переходов данного автомата будет иметь вид табл.13.
| A | B | C | D | |
| a | B,C | F | ||
| b | B | C,F |
Пустые клеточки говорят о том, что автомат частичный, а наличие сразу нескольких букв в одной клеточке – о том, что автомат недетерминированный. Для таких автоматов обычно предпочитают использовать не табличное и не графовые представления, а запись в виде так называемых продукций или грамматических правил, представленных в двух столбцах соответственно:
A → aB A:: = aB / bB / aC
A → bb B:: = bC / b
A → aC C:: = a
B → bC
B → b
C → a
Такого рода грамматики называют регулярными, или автоматными.
 2015-04-08
2015-04-08 2332
2332








