Для примера рассмотрим 4-е положение.
Ускорение точки А
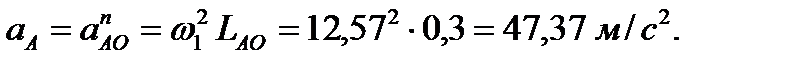
В общем случае 
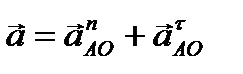 ,
,
но так как 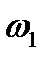 = const, то
= const, то 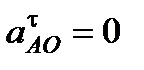 , поэтому
, поэтому 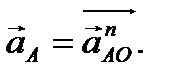
Принимаем длину отрезка 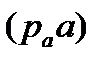 , изображающего вектор ускорения точки А, равной 100 мм, Тогда масштабный коэффициент плана ускорений
, изображающего вектор ускорения точки А, равной 100 мм, Тогда масштабный коэффициент плана ускорений
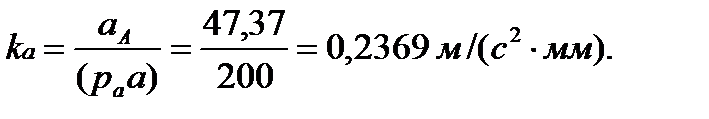
Рассматривая движение точки В вместе с точками А и C (переносное движение) относительно этих точек, получим векторные уравнения для построения ускорения точки:
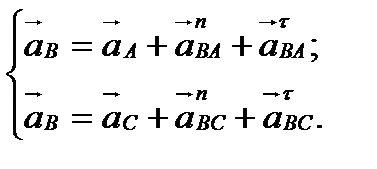
Первое уравнение: 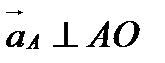 ;
;
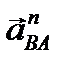 ║ АВ;
║ АВ; 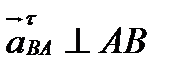 ;
;
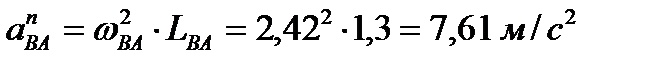
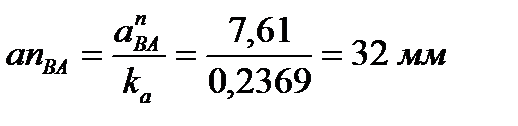
Второе уравнение: 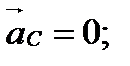
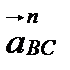 ║ ВC;
║ ВC; 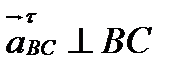 ;
;
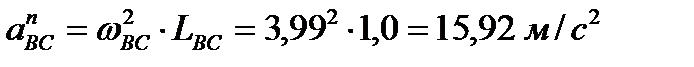
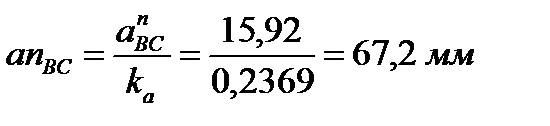
Величина (модуль) ускорения точки В
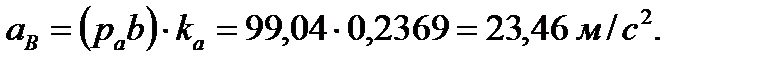

Ускорение точки D определяем по теореме подобия:
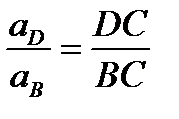 ;
;
Абсолютное ускорение точки D
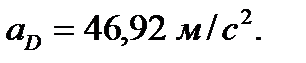
Векторные уравнения для нахождения ускорения точки F:
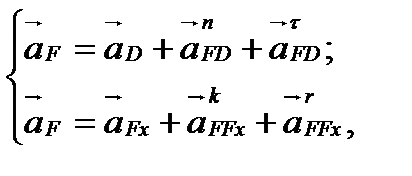
где 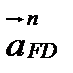 ║
║ 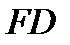 ;
; 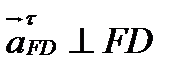 ;
;
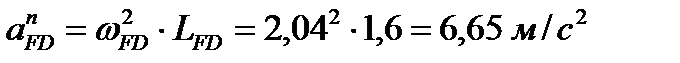
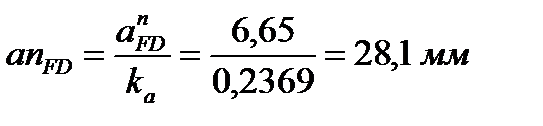
Абсолютное ускорение точки F
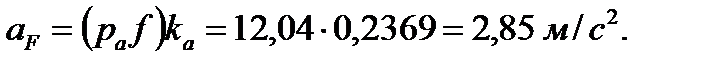
Определение ускорений центров тяжести звеньев производится с помощью теоремы подобия:
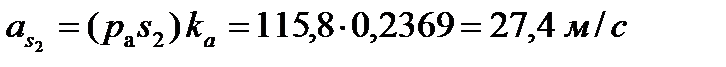
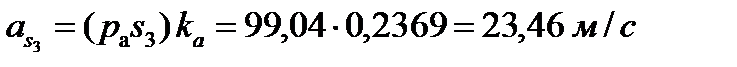
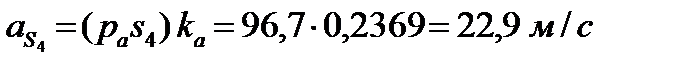
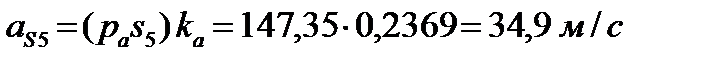
Определение угловых ускорений звеньев механизма:
Угловое ускорение звена 1 равно 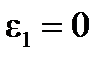 (так как
(так как 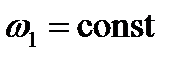 ),
),
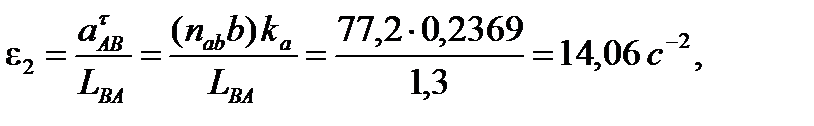
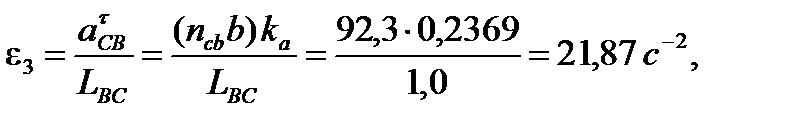
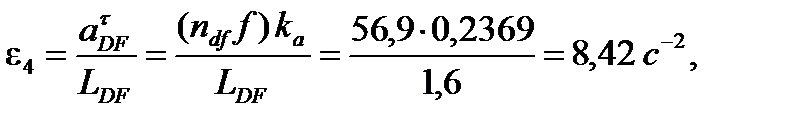
Для примера рассмотрим 9-е положение.
Ускорение точки А ka=0,4737 м/(с 2.мм).
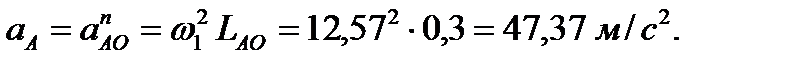
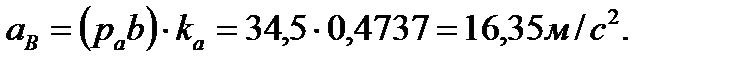
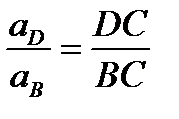 ;
;
Абсолютное ускорение точки D
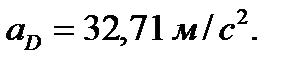
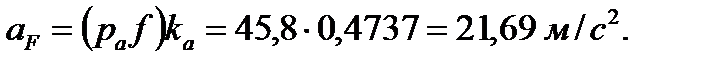
Определение ускорений центров тяжести звеньев производится с помощью теоремы подобия:
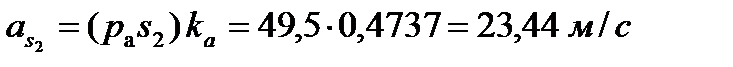
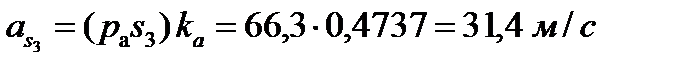
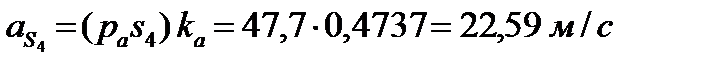
Определение угловых ускорений звеньев механизма:
Угловое ускорение звена 1 равно 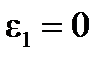 (так как
(так как 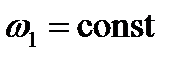 ),
),
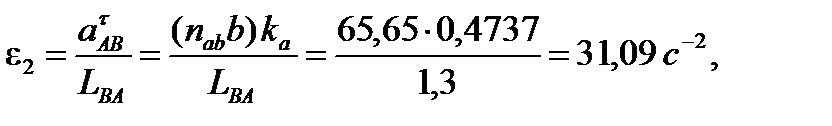
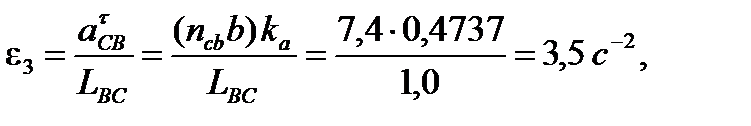
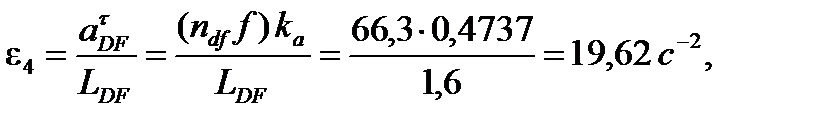
Кинематический анализ механизма методом графического дифференцирования.
Этим методом определяем величины скоростей, ускорений точки F механизма. Сначала строим диаграмму перемещений ползуна «SF ─ t» в функции времени. Диаграммы «VF ─ t» и «aF ─ t» строим методом графического дифференцирования соответственно диаграмм S = S(t) и V = V(t). Принимаем масштабный коэффициент 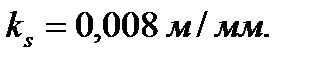
Время одного оборота кривошипа:
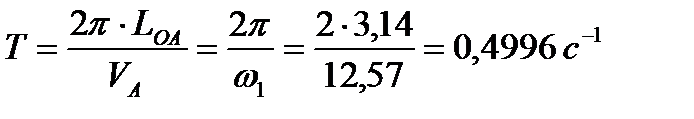
Вычислим масштабы:
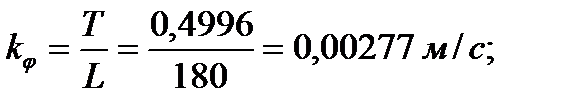
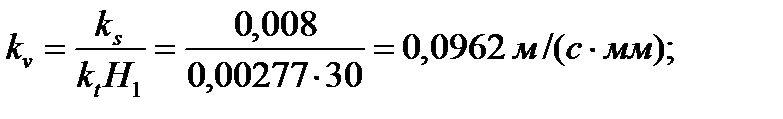
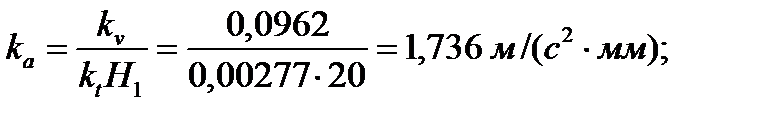
 2015-04-08
2015-04-08 294
294







