Общая характеристика и вычислительная схема метода МОХ

Метод Хюккеля.

Решение уравнения Хартри - Фока - Рутаана методом самосогласованного поля, без использования каких-либо других приближений, лежит в основе неэмпирических методов расчёта, которые отличаются используемым базисом атомных орбиталей.

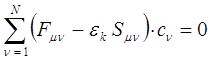
При использовании данных методов основные затраты машинного времени (обычно около 70% всего требуемого для полного расчета времени) направлены на вычисление интегралов межэлектронного взаимодействия фокиана:

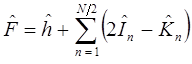
По мере увеличения размеров молекулы число таких интегралов возрастает примерно пропорционально N⁴, где N - размер базиса атомных орбиталей. Соответственно этому растут время и стоимость расчёта. Возможны два различных подхода, направленных на уменьшение вычислительных трудностей. Первый из них связан с пренебрежением части интегралов, входящих в выражение:

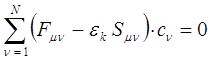
и сохранении во всём остальном общей вычислительной процедуры и порядка выполнения неэмпирического расчёта. Этот подход реализован в методе PRDDO, в котором сохраняются одно-, двух- и трёхцентровые кулоновские интегралы и одно- и двухцентровые обменные интегралы. Фактически из всех N⁴ интегралов остаются N³ интегралов. Метод PRDDO предложенный У. Липскомом в 1973 г. по точности лишь немного уступает неэмпирическим расчётам в базисе STO-3G.

В этом базисе каждая атомная орбталь, представленная в виде орбитали Слэйтера, апрксимируется тремя функциями гауссового типа:

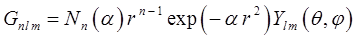
где N_n - нормировочный множитель, α – варьируемый параметр. Этот базис является минимальным, но достаточно удовлетворителен для воспроизведения молекулярной геометрии (ошибки в длинах связей 0,003 нм и углов ~ 4°). Другой подход, оказавшийся более перспективным, основан на замене большей части интегралов параметрами, взятыми из эксперимента - потенциалами ионизации атомов в орбитальных валентных состояниях и др., и использовании различных приближённых выражений, включающих параметры, для оценки интегралов. Основанные на этом подходе методы называются полуэмпирическими. Так, в приближении Хартри-Фока, фокиан 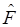для невырожденных электронных состояний полносимметричен, что означает, что матричные элементы фокиана на орбиталях разного типа симметрии согласно теореме Вигнера-Эккарта должны быть равны нулю. Если базис, в котором представлены молекулярные орбитали разбит на два базисных набора (или может быть сведён к таким наборам) симметричных и антисимметричных функций, то матричные элементы фокиана:

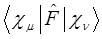
будут равны нулю, если и разного типа симметрии, и будут отличны от нуля в противном случае. Это означает, что матрица фокиана, как и матрица интегралов перекрывания, имеет блочно-диагональный вид:

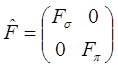
И хотя матричные элементы в каждом блоке за счёт двухэлектронных интегралов зависят от всего набора орбиталей 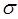– и , и 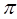, тем не менее, задачу можно решать итерациями, сначала определяя 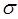-орбитали, затем – 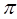-орбитали, затем вновь возвращаясь к определению 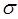-орбиталей и т.п. Если же считать 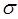-орбитали приближённо известными на основе модельных представлений, то можно в конечном итоге ограничиться рассмотрением лишь 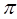-блока. 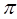-Электроны отличаются от 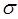-электронов не только свойствами симметрии. Прежде всего, каждая группа электронов движется в различных частях молекулы. 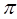-Электроны имеют равную нулю вероятность нахождения в плоскости молекулы, в то время как 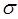-электроны имеют максимальную вероятность нахождения в этой плоскости. 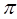-Электроны обычно связаны с молекулой слабее, чем 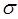-электроны, так что они более поляризованы, легче ионизируются и обладают большей реакционной способностью, а поэтому в большей мере ответственны за химические и физические свойства 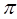-электронных соединений (электронные спектры, потенциалы ионизации и т.д.). Кроме этого, состояния 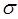-электронов можно локализовать в пространстве, и поэтому их можно отнести к связям между парами соседних атомов либо к «неподеленным» электронным пара на отдельных атомах, в то время как 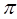-электроны образуют делокализованную систему в области сопряженного скелета молекулы. В методе молекулярных орбиталей Хюккеля (МОХ) полностью пренебрегают интегралами межэлектронного отталкивания. При этом условии матричные элементы оператора Фока очевидно будут совпадать с матричными элементами самого остова:

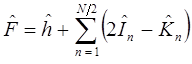
при условии, что:

оператор Фока очевидно будет сводиться к электронному Гамильтониану и таким образом, соответственно выражение вида:

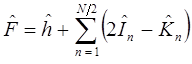
преобразуется соответственно к виду:

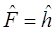
При рассмотрении свойств систем с сопряжёнными связями, в частности полиенов и ароматических углеводородов, широко используются различные приближённые полуэмпирические методы. Первым методом молекулярных орбиталей, который можно было использовать для расчёта свойств многоатомных молекул, явился метод МО Хюккеля, в основе которого лежат представления о гибридизации орбиталей атома углерода. Так, свободный атом углерода имеет шесть электронов с конфигурацией:

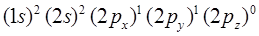
Постулируется, что один из 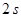- электронов атома углерода переходит на незанятую 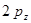- атомную орбиталь, в результате чего последний приобретает конфигурацию:

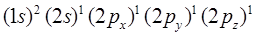
При образовании двойной связи орбитал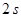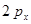и , и 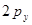превра­щаются в смешанные (гибридные) атомные орбитали, располагающиеся в одной плоскости под углом 120⁰ по отношению друг к другу. Они называются 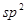- гибридными (тригональными) орбиталями. Каж­дый атом углерода использует две из трёх 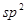- гибридных орбиталей на образование 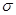- связей с двумя соседними атомами углерода, а третью орбиталь — на образование 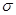- связи 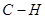. Все гибридные орбитали с 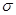- связями имеют максимальную элек­тронную плотность в плоскости молекулы. Поскольку каждый атом углерода в 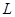- оболочке (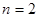) имеет четыре электрона, три из кото­рых находятся в состоянии 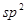- гибридизации, четвёртый электрон должен располагаться на 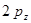- орбитали. В дальнейшем предполагается, что углерод – углеродная двойная связь состоит из 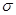- связи, образованной за счёт 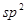- гибридных атомных орбиталей и 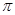- связи, образованной за счёт 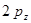- атомных орбиталей. Такое предположение ни в коей мере не является самоочевидным. Полинг, например, в одной из своих работ показал, что электроны атома углерода в его обычных валентных состояниях могут промотироваться на значительно более высокие уровни и что орбитали связей могут в заметной степени приобретать 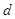- и даже 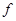-характер. Действительно, несмотря на то, что 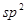- орбитали должны располагаться под углом 120° друг к другу, в некоторых молекулах валентный угол отличается от этого значения. Так, экспериментально определен­ные углы между связями 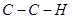в этилене, бутадиене, аллене и бутатриене составляют 121,3; 119,8; 120,8 и 121,5⁰ соответственно. Тем не менее, рамках данной работы, удобнее использовать более простое представление о 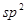- гибридизации. Характерные свойства сопряженных и ароматических систем обусловлены системой - электронов, возникающей за счёт 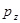- AO. Эти атомные орбитали образуют молекулярные орбитали, на которых 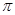- электроны не локализованы у какого-либо отдельного атома или связи, а, движутся свободно по всей молекуле. При расчёте молекул методом МО обычно пренебрегают 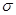- электронами, относя их к остову молекулы. 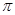-Электроны описы­вают с помощью молекулярных орбиталей, состоящих исключительно из атомных 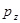- орбиталей, например слэйтеровского типа. Рассматривая молекулы сопряжённых и ароматических углеводородов, мы будем в основном обсуждать поведение 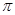- электронов. Предположение, что систему 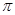- электронов можно рассчитать независимо от 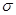- электронов, основано на различии в симметрии соответствующих молекулярных орбиталей. 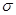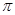Как известно - и - орбитали распределены в различных областях пространства и обладают различными свойствами симметрии. Так, 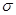- молекулярная орбиталь лежит в плоскости молекулы и симметрична относительно поворота на угол 180⁰ вокруг межъядерной оси, а 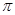- орбиталь, располагающаяся ортогонально по отношению к плоскости 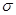- орбитали, является антисимметричной относительно такого поворота. В связи с различными свойствами симметрии соответствующих молекулярных орбиталей, 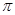- электроны можно рассматривать независимо от 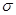- электронов, проводя расчёты электронной структуры молекул сопряжённых систем в так называемом 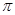- электронном приближении. Согласно такому предположению, 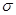- связи образуют более или менее жёсткий остов, в котором и движутся 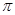- электроны. Такое разделение орбиталей можно показать на примере этилена или бензола, но оно менее строго в случае анилина и некоторых других соединений, в которых орбитали не полностью ортогональны. 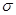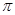Однако точные неэмпирические расчёты показывают, что раздельное рассмотрение - и - электронов не совсем корректно. 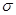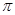В работах ряда учёных было показано, что даже в молекуле бензола - и - электронные системы разделены не пол­ностью. 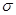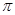Между - и - электронами существует определённое взаимодействие (учитываемое в более точных расчётных схемах), пренебрежение которым приводит к заметным ошибкам. Однако, несмотря на весьма упрощенное представление, подход предложенный Хюккелем оказался достаточно удачным. Применение его к молекулам соединений с сопряжёнными связями и ароматическим соединениям позволило получить простым путём важные результаты, не при­бегая к точным квантово – механическим расчётам. Основные положения и расчётная схема метода Хюккеля были построены на основании её сходства с формализмом теории Слэйтера и Блоха для описания поведения электронов в металлах. Поскольку в методе Хюккеля 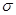- связи не рассматриваются, вместо структурных формул используют так называемые молекулярные графы. Вершины графа соответствуют атомам углерода, а рёбра – углерод – углеродным связям. Так как связь между атомами углерода и водорода 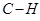является 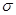- связью, атомы водорода не изображают на графе и не принимают во внимание при расчётах. Информацию о связях между атомами углерода передаёт также топологическая матрица 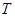. Она представляет собой симметричную матрицу 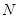- го порядка, элементы которой равны единице, если атомы связаны друг с другом, и равны нулю, если они непосредственно не связаны между собой. Таким образом, топологическая матрица 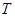, состоит только из 1 и 0. Нумерация вершин графа (атомов) соответствует нумерации строк и столбцов топологической матрицы. Информация, содержащаяся в топологической матрице, эквивалентна сведениям, которые несёт в себе структурная формула молекулы; последующий её анализ и математическая переработка позволяют получить сведения относительно распределения электронного заряда, порядков связей, величин свободных валентностей в молекуле. Привлекательность метода предложенного Хюккелем заключается в том, что его использование не требует использования ЭВМ и вполне оказывается достаточным иметь микрокалькулятор. Метод МОХ позволяет осуществить расчёты в полной мере и пояснить принципы, на которых основаны и расчёты более сложными методами ССП – ЛКАО – МО. Наиболее яркой демонстрацией успеха метода МОХ, его описательных и предсказательных возможностей, является расчёт энергетических уровней и относительной устойчивости сопряжённых систем – молекул линейных и циклических полиенов. Метод молекулярных орбиталей предложенный Э. Хюккелем в 1931 г. относится к простейшим полуэмпирическим методам квантовой химии. В методе МОХ вводится ряд упрощающих предположений (в частности полное пренебрежение всеми интегралами межэлектронного отталкивания, на расчёт которых в точных неэмпирических квантовохимических методах затрачивается до 70 % машинного времени), благодаря которым решение векового детерминанта становится общедоступным. Метод МОХ появился раньше, чем метод ССП Хартри – Фока, поэтому многие полуэмпирические методы расчёта типа ЛКАО – МО были введены не путём упрощения метода самосогласованного поля (ССП), а как обобщения метода Хюккеля. Молекулярные орбитали в приближении Хюккеля являются собственными функциями 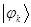одноэлектронного гамильтониана 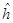, их находят, решая задачу на собственные значения этого оператора. В общем случае, каждая молекулярная орбиталь 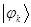может быть записана в виде линейной комбинации 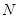атомных орбиталей 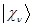, например слэйтеровского типа:

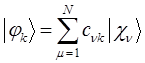
Полная волновая функция 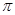- электронной системы записывается в виде произведения одноэлектронных волновых функций 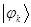(молекулярных орбиталей):

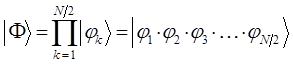
где 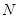- общее число электронов в 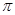- электронной системе. Поскольку здесь каждый атом углерода поставляет одну 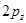- атомную орбиталь для образования молекулярной орбитали и один 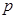-электрон в общую 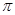- электронную систему, тогда число 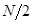будет представлять собой число занятых электронами молекулярных орбиталей. Свободные орбитали сюда не включают. Полная энергия 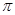- электронной системы, очевидно, будет равна:

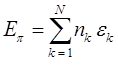
где 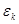- орбитальная энергия, а 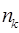- число заполнения электронами орбитали с номером 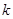, которое может принимать значения:

ü для полностью заполненной молекулярной орбитали ;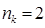

ü для наполовину заполненной молекулярной орбитали ;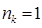

ü для свободных (вакантных) молекулярных орбиталей .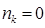

Не трудно заметить, что в выражении для полной 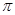- электронной энергии:

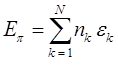
отсутствуют слагаемые, отвечающие за межэлектронное отталкивание. Это существенный недостаток метода Хюккеля. Несмотря на это он занимает прочное положение в ряду полуэмпирических расчётных методов квантовой химии, удовлетворительно, на качественном уровне описывая электронное строение и свойства молекул органических соединений. Учитывая разложение молекулярной орбитали 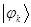по базисному набору функций :

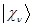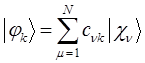
а также учитывая, что:

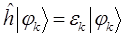
будем иметь соответственно:

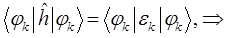
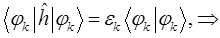
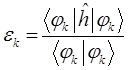
Подставляя в полученное уравнение для орбитальной энергии разложение одноэлектронной волновой функции по базисному набору соответствующих базисных функци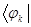й и :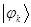

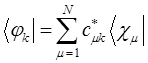
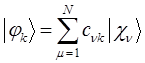
будем иметь соответственно:

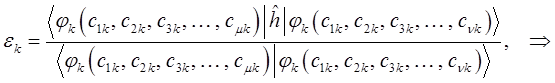
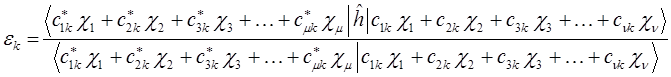
или в общем виде:

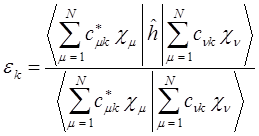
откуда:

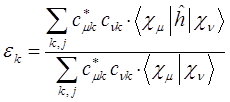
Введём следующие обозначения:

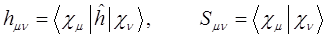
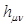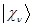здесь называют матричными элементами гамильтониана в базисе атомных орбиталей и , а 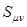- есть интеграл перекрывания. Их физический смысл зависит от природы базисных функци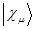й и 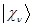. Выражение для средней энергии, полученное выше, с учётом приведенных выше обозначений, можно очевидно представить к виду:

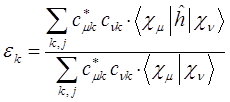
откуда следует, что:

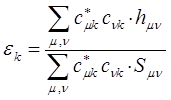
т.е. имеем соответственно:

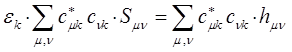
и далее вариационные коэффициенты находят из условия:

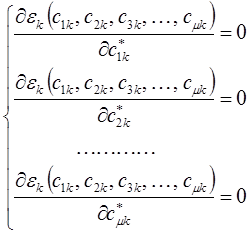
Для этого продифференцируем полученное выражение по коэффициенту :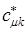

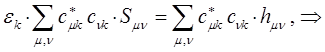
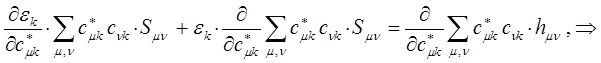
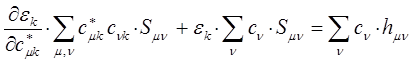
учитывая, что производная от энергии по вариационному коэффициенту 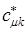равна нулю в точке экстремума:

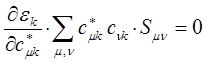
полученное в ходе дифференцирования выражение, можно представить далее соответственно к виду:

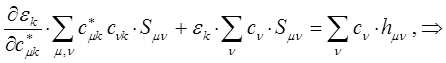
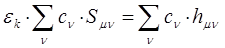
или после соответствующих преобразований:

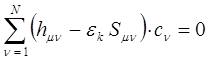
Полученную выше систему линейных уравнений можно конкретизировать, представив последнюю к виду:

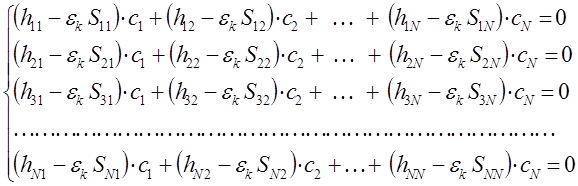
или в матричной форме:

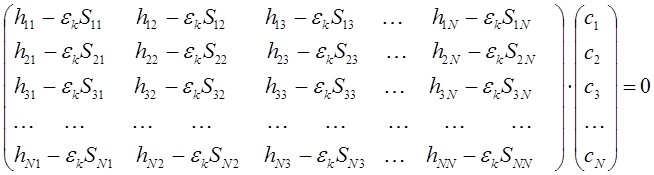
полученная в ходе проделанных выше выкладок система уравнений:

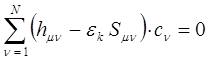
может быть преобразована далее к виду:

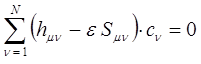
или с учётом условия:

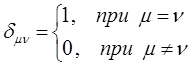
имеем соответственно:

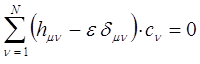
здесь:

В ходе проделанных выше выкладок мы пришли к системе линейных уравнений:

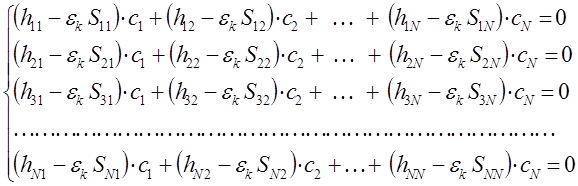
или в матричном виде:

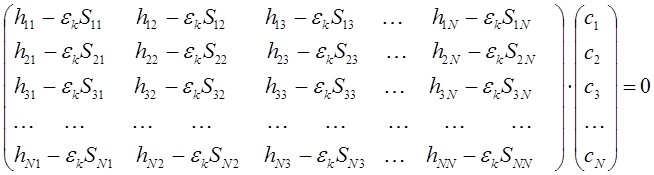
Полученная выше система уравнений имеет нетривиальные решения при условии, если детерминант, составленный из коэффициентов при неизвестных, равен нулю. Имеем таким образом соответственно:

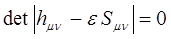
Матричные коэффициенты одноэлектронного гамильтониана 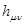в приближении Хюккеля (МОХ) не вычисляют, а заменяют параметрами, которые берут либо из эксперимента, либо оценивают, сопоставляя с другими, более строгими теоретическими методами. Диагональные матричные элементы одноэлектронного гамильтониана заменяют параметром 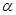(кулоновский интеграл):

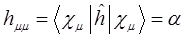
На языке квантовой механики данный параметр передаёт классическое кулоновское взаимодействие частиц. Он включает в себя энергию электрона в атоме водорода в основном состоянии, кулоновское отталкивание ядер для случая молекул и энергию кулоновского взаимодействия одного из ядер многоэлектронной системы с электронным облаком окружающем другое ядро. На расстояниях порядка равновесного межъядерного и выше, этот интеграл отрицателен и на больших, где отталкивание ядер мало, равен энергии электрона атомной орбитали 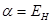. Это означает, что кулоновский интеграл приближённо равен энергии электрона в атоме водорода и на основании теоремы Купманса, его можно оценить по значению энергии ионизации атомной орбитали. В данном случае его значение можно оценить по значению ионизационного потенциала 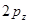- орбитали атома углерода и составляет 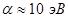. Причём 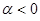и, только на очень малых расстояниях по-сравнению с равновесным, он становится положительным и неограниченно возрастает. Недиагональные матричные элементы заменяют параметром 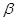, называемым также обменным (резонансным) интегралом.

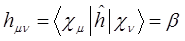
Энергия, выражаемая интегралом 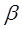, не имеет аналога в классической механике. В общем случае интеграл 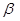описывает то добавочное понижение энергии, которое возникает из-за возможности перехода электрона от ядра одного атома к ядру другого атома, возможности движения электрона в поле двух ядер. При этом происходит как бы «обмен» ядер, обмен состояния 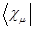на состояние 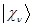. Возникновение такого рода обменных сил формально может быть связано с эрмитовостью оператора Гамильтона 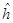. Этот интеграл на бесконечности равен нулю, на всех других, кроме ультракоротких – всегда отрицателен, т.е. 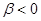. Только на очень коротких расстояниях, достаточных для возникновения химической связи он становится положительным и возрастает неограниченно. Именно на таких расстояниях становится возможным возникновение обменных сил и как следствие – образование химической связи. Именно его вклад и определяет энергию химической связи: чем он больше, тем прочнее будет химическая связь. Для связанных между собой атомов параметр 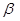отличен от нуля, а для несвязанных – равен нулю. Такое приближение называют приближением ближайших соседей:

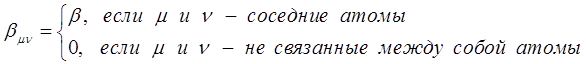
Кулоновские интегралы одинаковы для всех атомов углерода, а резонансные интегралы 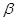одинаковы для всех углерод – углеродных связей, 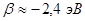. Параметр 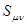называется интегралом перекрывания. Этот интеграл служит мерой перекрывания атомных орбиталей, образующих молекулярную орбиталь.

Интеграл перекрывания – безразмерная величина, он может принимать два значения:

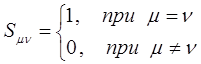
а также:

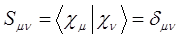
Он равен единице, при 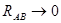и спадает до нуля, при возрастании межъядерного расстояния 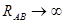. При увеличении 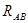, величина интеграла перекрывания убывает экспоненциально. В общем случае, на расстояниях между атомами, существующими в молекулах, обменный интеграл тем больше по абсолютной величине, чем больше интеграл перекрывания. Между обменным интегралом и интегралом перекрывания существует линейная зависимость 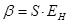. Принято считать, что чем больше перекрываются атомные орбитали соответствующих атомов, партнёров по связи, образующих молекулярные орбитали, тем прочнее связь. Это утверждение лежит в основе принципа максимального перекрывания. Требование, чтобы атомные орбитали перекрывались при образовании молекулярных орбиталей, есть, таким образом, требованием, чтобы расположение атомных ядер в молекуле отвечало максимальной её устойчивости. В методе молекулярных орбиталей Хюккеля интегралом перекрывания пренебрегают. Действительно, максимальное значение этого интеграла равно единице, а теоретически рассчитанное его значение, вычисленное с 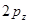- орбиталями атома углерода составляет 0,277. Из соображений малости данной величины, в методе МОХ ею пренебрегают, принимая её равной нулю. Такое пренебрежение наряду с заменой матричных элементов гамильтониана параметрам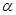и и 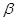, существенно упрощает расчёт. Для общего случая будем иметь соответственно:

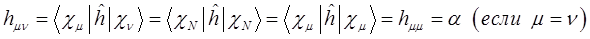
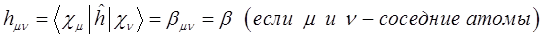
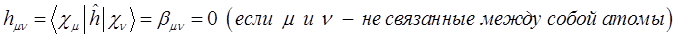
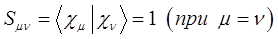
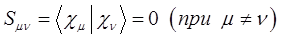
или с учётом введенных параметров, уравнения для нахождения орбитальных коэффициентов можно переписать в виде:

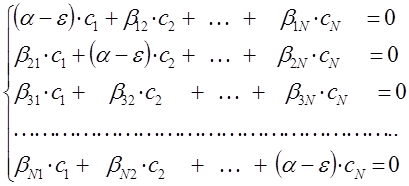
полученную выше систему вековых уравнений можно представить далее к виду:

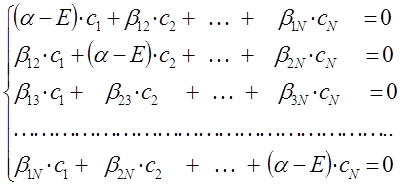
Такое преобразование, очевидно, является эквивалентным операции транспонирования матриц. Полученная выше система уравнений будет справедлива при условии, если вековой детерминант, составленный из коэффициентов при неизвестных, будет равен нулю:

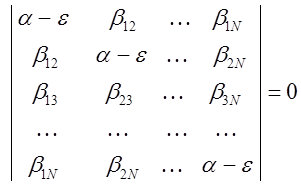
Вид хюккелевского детерминанта можно несколько упростить. Для этого каждый элемент детерминанта разделим на 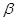и введём обозначение:

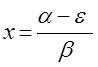
значение x называют орбитальным параметром. Из полученного соотношения следует, что:

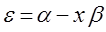
если известны значения x, можно определить значения орбитальных энергий E.

В методе Хюккеля их выражают в единицах 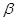. Если предположить, что 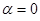, тогда выражение:

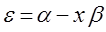
с учётом:

может быть переписано в виде:

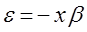
При этом если 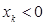, то получаемая молекулярная орбиталь будет являться связывающей; если 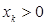, то получаемая молекулярная орбиталь будет являться разрыхляющей; если же 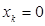, то получаемая молекулярная орбиталь будет являться несвязывающей. Очевидно, чем меньшее значение будет принимать орбитальный параметр 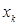, тем в большей степени у неё будут выражены связывающие свойства и соответственно, чем большие значения будет принимать орбитальный параметр 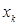, тем в большей степени будут выражены у молекулярной орбитали разрыхляющие свойства. Если число связывающих молекулярных орбиталей принять равным 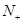, число разрыхляющих - 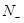, а число несвязывающих -

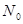, то очевидно их сумма будет равна общему числу атомов углерода 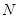в сопряжённой системе:

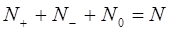
энергии же молекулярных орбиталей в методе Хюккеля для сопряжённых систем будут расположены в интервале:

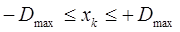
В полученном выше неравенстве 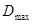представляет собой максимальное число рёбер (связей), выходящих из вершин (атомов) соответствующего молекулярного графа и 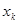- орбитальный параметр. Для линейных полиенов 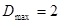, для циклических сопряжённых систем 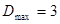. Необходимо отметить, что хюккелевский детерминант легко можно составить на основе молекулярного графа, не расписывая подробно выражение:

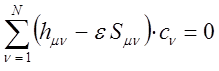
для этого необходимо придерживаться следующих основных действий:

1. Прежде чем составить хюккелевский детерминант, изображают граф молекулы и нумеруют атомы углерода, входящие в её состав.

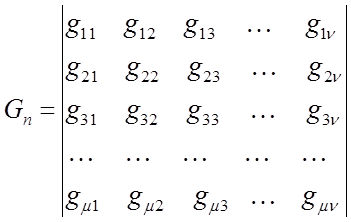
На основании данных о молекулярном графе и виде топологической матрицы (или матрицы смежности), передающих информацию о молекулярной структуре сопряжённых и ароматических соединений, а также с учётом введенного уже выше орбитального параметра 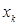, составляют хюккелевский детерминант, порядок которого очевидно будет равен общему числу атомов углерода в молекуле:

2. Полагаем значения диагональных матричных элементов равными 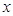и далее, в соответствии с приближением МОХ, присваиваем значение 1 тем недиагональным матричным элементам, которые соответствуют соседним атомам (например, первому и второму) и нуль тем недиагональным матричным элементам, которые отвечают не соседним атомам (например, первому и третьему). В первом случае между атомами имеется химическая связь, во втором случае – если связи между атомами нет. Так, для молекул линейных полиенов, вековой детерминант будет очевидно будет иметь вид:

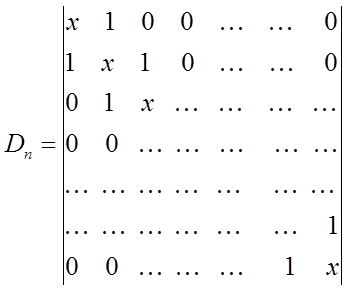
3. Полученный таким образом вековой детерминант приравнивают к нулю.

4. На основании хюккелевского детерминанта находят значения орбитальных параметров и энергий молекулы и далее составляют уравнения для нахождения орбитальных коэффициентов. Для этого матричные элементы каждой строки детерминанта поочерёдно умножают на соответствующий орбитальный коэффициент, полученные произведения складывают, а сумму приравнивают к нулю. Число уравнений должно совпадать с порядком детерминанта. Расчёты сопряжённых систем показывают, что сложность, а, следовательно, и время, затрачиваемое на вычисления, растут пропорционально увеличению числа атомов углерода в молекуле. Однако существует и другой путь решения векового детерминанта, который основан на свойствах самих определителей и приводит к отысканию полинома порядка N -го порядка:

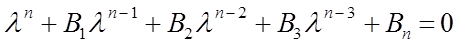
Применительно к молекулам линейных полиенов – углеводородов с открытой цепью общей формулы 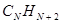и чередующимися (альтернирующими) двойными и одинарными связями, хюккелевский детерминант очевидно будет иметь вид:

Понижение порядка детерминанта такого типа, когда число атомов углерода в молекуле полиена 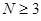, производится по формуле:

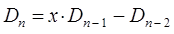
Вычисления детерминанта 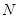-го порядка 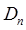приводят к следующим формулам для детерминантов различных порядков:

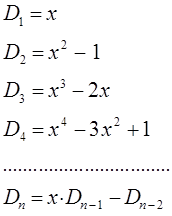
Как это хорошо видно, полиномы полученной выше последовательности подобны полиномам Чебышева от аргумента :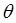

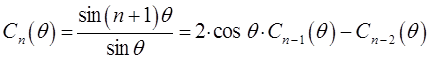
тогда соответственно:

или в общем виде:

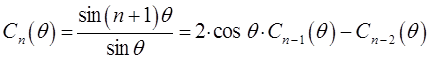
Из сравнения выражений:

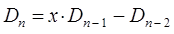
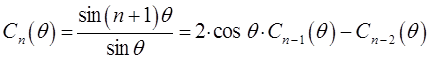
становится очевидным, что если положить:

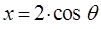
то

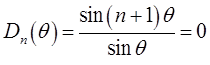
что удовлетворяется при условии:

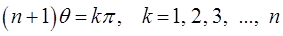
откуда:

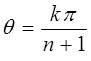
или после подстановки значения для 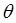в выражение:

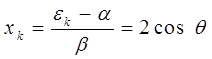
будем иметь соответственно:

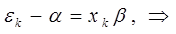
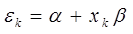
откуда:

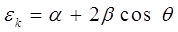
или после подстановки значения:

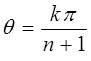
в выражение:

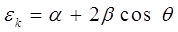
получим в окончательном виде:

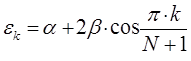
здесь 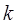- индекс молекулярной орбитали, 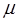- индекс атомной орбитали и 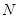- число атомов углерода в цепи сопряжения. А. Фрост и Б. Мисулин предложили простой и полезный графический образ такого рода решений, известный также как «круг Фроста». Так, если первую половину окружности радиусом 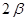разделить на 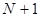равных дуг, то ординаты точек деления, за исключением, лежащих на вертикальном диаметре, будут соответствовать орбитальным энергиям полиена.

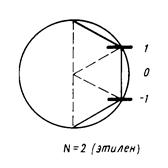
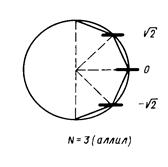
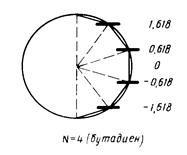
Рис. 14. Методы графического изображения для общих решений векового детерминанта (круг Фроста).

Действительно, если первую половину окружности радиусом 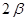разделить на 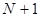равных дуг, то ординаты точек деления, за исключением, лежащих на вертикальном диаметре, будут соответствовать орбитальным энергиям полиена.

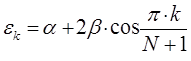
Выражения для молекулярных орбиталей и соответствующих им орбитальных энергий после проведения расчётов сводят в таблицу и на основании полученных данных строят энергетические диаграммы, отражающие строение молекулы рассматриваемой сопряжённой системы и далее, проводят вычисления дескрипторов (числовых характеристик) молекулярной структуры, которые для наглядности наносят на молекулярные диаграммы (графы).