Проверка адекватности моделей ARMA

Для проверки адекватности моделей ARMA используются несколько критериев. Прежде всего, в построенной модели с помощью обычного t -критерия можно проверить статистическую значимость ее параметров.

Кроме того, в соответствии с предположениями, лежащими в основе построения модели, случайные составляющие 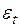являются белым шумом. Следовательно, остатки регрессии 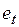, являющиеся оценками 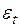, должны быть одной из возможных реализаций белого шума, т.е. иметь нулевую автокорреляцию и нулевое среднее (если модель содержит константу). Поэтому выборочная автокорреляционная функция остатков, вычисляемая по формуле

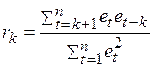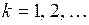, , (4.55)

при больших 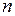имеет распределение, близкое к нормальному 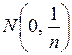. Если значение 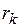окажется вне интервала 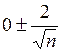, то на 95%-м уровне значимости отвергается гипотеза равенства его нулю.

Для проверки гипотезы о равенстве нулю сразу 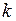первых значений автокорреляционной функции остатков используется уже известная нам Q - статистика Бокса – Пирса, вычисляемая по формуле

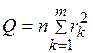. (4.56)

Смысл проверки тот же самый, только проверяется автокоррелированность остатков, а не моделируемого показателя. При нулевой гипотезе, предполагающей отсутствие автокорреляции в остатках, статистика Q имеет распределение 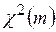. Если расчетное значение Q -статистики превосходит соответствующее значение 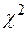, то нулевая гипотеза отвергается.

Если тесты показывают наличие автокорреляции в остатках, то рассматриваемаямодель ARMA неадекватна, ее необходимо модифицировать.

В тех случаях, когда одновременно несколько моделей ARMA, оказываются адекватными данным, то среди построенных моделей рекомендуется выбирать наиболее простую модель, содержащую наименьшее количество параметров.

Во многих компьютерных пакетах рассчитывается значение критерия Акаике (AIC) по формуле

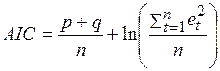, (4.57)

в которой комбинируются два требования к модели: сложность и точность (более сложной считается модель с большим числом параметров). В соответствии с этим критерием выбирается та модель, для которой значение AIC меньше.

Для этих же целей используется критерий Шварца

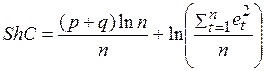. (4.58)

Оба критерия позволяют выбрать более сложную модель только в том случае, когда ее точность значительно превосходит точность менее сложной.