Построение моделей ARIMA

Построение моделей ARIMA осуществляется в несколько этапов.

1. На первом этапе проводится идентификация модели. Для этого ряд тестируется на стационарность с целью определения степени его интеграции. Для тестирования используется критерий Дики – Фуллера (DF), с помощью которого определяется, равно ли значение коэффициента 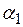единице или оно меньше единицы в модели без свободного члена

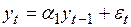. (4.41)

Если 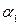равно единицы, то данные имеют единичный корень и степень его интеграции равно единице, т.е. степень интеграции равна единице, и мы имеем дело с рядом I (1). Если же 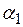меньше единицы, то ряд стационарен, т.е. I (0). Суть критерия сводится к проверке нулевой гипотезы

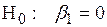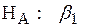значительно меньше нуля. (4.42)

Нулевая гипотеза отвергается, если статистика 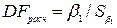меньше критического значения из таблиц Дики и Фуллера, которое для 1%-го уровня значимости равно -2,58 (для 5%-го уровня значимости равно -1,95). Используемый в этом критерии параметр 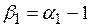, а 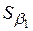– стандартная ошибка 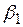, а само 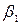определяется как параметр уравнения

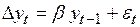. (4.43)

Проверка на стационарность похожа на использование традиционного t -критерия, однако применение t -критерия слишком часто отвергает нулевую гипотезу в ситуациях, когда она справедлива. Кроме того, проверка стационарности осложняется в тех случаях, когда существует автокорреляция остатков. Проблема автокорреляции остатков решается применением расширенного критерия Дики – Фуллера (EDF), в котором критическое значение, с которым сравнивается 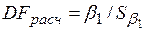, определяется по формуле, учитывающей размер выборки

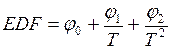. (4.44)

Значения составляющих (4.44) в зависимости от уровня значимости следующие:

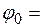
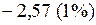или ;

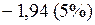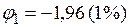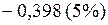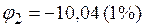или .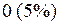

Если нулевая гипотеза проверяется для модели со свободным членом

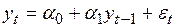, (4.45)

то строится уравнение

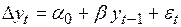(4.46)

и расчетное значение 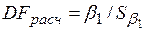сравнивается с критическим значением EDF, рассчитываемым при

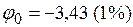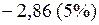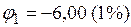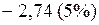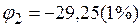или ;

или .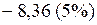

В тех случаях, когда модель содержит и свободный член, и тренд

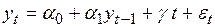, (4.47)

то коэффициент 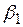определяется по уравнению

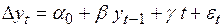, (4.48)

а критическое значение для проверки нулевой гипотезы рассчитывается при

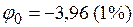или ;

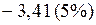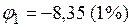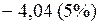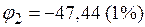или .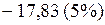

Если в результате проверки на единичный корень нулевая гипотеза (ряд нестационарный) принимается в качестве рабочей, то применяют операцию взятия разности и повторяют тестирование.

2. После того, как получено подтверждение о стационарности исходного временного ряда или его разностного представления, для стационарного ряда строят выборочные автокорреляционные и частные автокорреляционные функции, с помощью которых формулируются гипотезы о возможных порядках авторегрессии (р) и скользящего среднего (q).

Для каждой из выбранных в соответствии с выдвинутыми гипотезами моделей оцениваются параметры и вычисляются остатки. Затем все построенные модели проверяются на адекватность и из моделей, адекватных данным, выбирается самая простая, т.е. та, которая имеет наименьшее количество параметров.

3. Методы для оценивания параметров выбираются в зависимости от сложности модели. Если в модели присутствует только авторегрессионная часть, то ее параметры можно оценивать с помощью МНК. Если же оцениваются параметры комбинированной модели, то возникают различные ситуации. Например, для модели ARMA (1, 1)

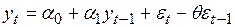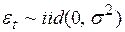, , (4.49)

которую можно представить, используя оператор сдвига 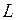(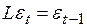) в виде

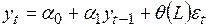, (4.50)

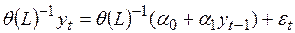, (4.51)

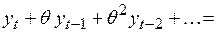
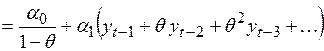, (4.52)

где 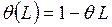и .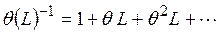

Одним из возможных подходов к построению моделей ARMA (1, 1) заключается в следующем: приравниваются нулю все значения, предшествующие началу наблюдений, т.е. 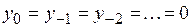. Тогда замена переменных

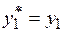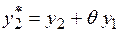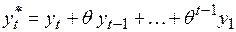, ,..., (4.53)

позволяет записать рассматриваемую модель в виде

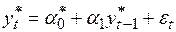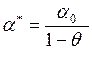, . (4.54)

В том случае, когда 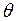известно, параметры этой модели можно оценивать с помощью метода наименьших квадратов. В общем случае модель нелинейна по параметрам и для их оценки используется условный метод максимального правдоподобия или полный метод максимального правдоподобия. Оба метода фактически сводятся к решению нелинейных систем уравнений.

Эффективным приемом построения подобных моделей для прогнозных целей является подход, основанный на подборе параметра 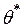, обеспечивающего минимальную ошибку постпрогнозных расчетов. Этот подход является составной частью построения адаптивных моделей прогнозирования и, поэтому будет подробно рассмотрен в главе, которая посвящена адаптивным методам.