Задание 5.Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,1. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Решение:
Пусть А – «выбранная ручка пишет хорошо»,
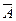 – «выбранная ручка пишет плохо (или не пишет)».
По условию задачи Р( – «выбранная ручка пишет плохо (или не пишет)».
По условию задачи Р(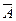 ) = 0,1.
Значит, вероятность того, что выбранная ручка пишет хорошо, по формуле вероятности противоположного события равна: Р(А) = 1 – Р( ) = 0,1.
Значит, вероятность того, что выбранная ручка пишет хорошо, по формуле вероятности противоположного события равна: Р(А) = 1 – Р(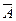 ) = 1 – 0,1 = 0,9.
В бланк ответов: 0,9 ) = 1 – 0,1 = 0,9.
В бланк ответов: 0,9
|
Пример 39.
Задание 5. Вероятность попадания в мишень при одном выстреле равна 0,8. Было произведено 3 независимых друг от друга выстрела. Найти вероятность того, что мишень будет поражена хотя бы раз.
Решение:
Пусть А – «мишень поражена при первом выстреле», В – «мишень поражена при втором выстреле», С - «мишень поражена при третьем выстреле». Тогда 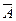 - промах. По условию Р(А) = 0,8, значит, Р( - промах. По условию Р(А) = 0,8, значит, Р( 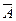 ) =1 – 0,8 = 0,2. События А,В, С попарно независимы.
Вероятность того, что мишень будет поражена хотя бы раз, если произошло или А, или В, или С, т.е. произошло событие А+В+С, определим «через отрицание».
Тогда ) =1 – 0,8 = 0,2. События А,В, С попарно независимы.
Вероятность того, что мишень будет поражена хотя бы раз, если произошло или А, или В, или С, т.е. произошло событие А+В+С, определим «через отрицание».
Тогда 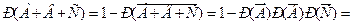 1- 0,2³ = 0,992,
т.к. одновременно происходят события 1- 0,2³ = 0,992,
т.к. одновременно происходят события 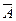 , , 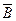 , , 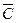 , т.е. , т.е. 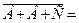 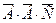 , где событие , где событие 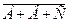 - «мишень не будет поражена».
В бланк ответов: 0,992 - «мишень не будет поражена».
В бланк ответов: 0,992
|
Формула сложения вероятностей для несовместных событий:
Р(А+В) = Р(А) + Р(В).
Суммой событий А и В называют событие А+В, состоящее в появлении либо события А, либо только события В, либо и события А и события В одновременно.
 2015-04-12
2015-04-12 359
359








