1 – 10. Вычислить определитель:
а) непосредственным разложением по 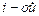 строке;
строке;
б) непосредственным разложением по 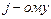 столбцу.
столбцу.
1. 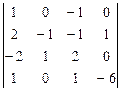 2.
2. 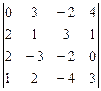 3.
3. 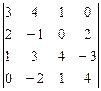
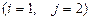
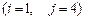
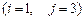
4. 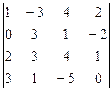 5.
5. 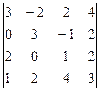 6.
6. 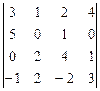
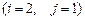
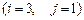
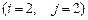
7. 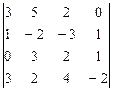 8.
8. 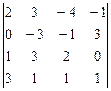 9.
9. 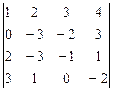
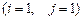
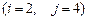
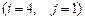
10. 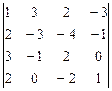
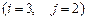
11 – 20. Найтиматрицу 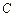 , если
, если 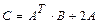 .
.
11. 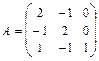 ,
, 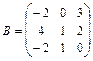 12.
12. 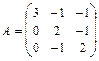 ,
, 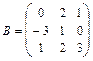
13. 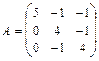 ,
, 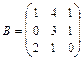 14.
14. 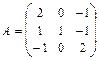 ,
, 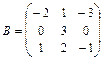
15. 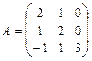 ,
, 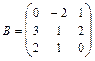 16.
16. 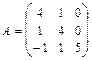 ,
, 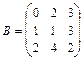
17. 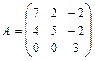 ,
, 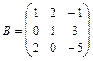 18.
18. 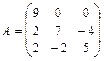 ,
, 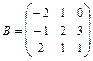
19. 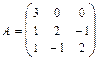 ,
, 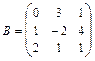 20.
20. 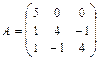 ,
, 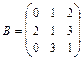 .
.
21 – 30. Найтисобственные числа и собственные векторы матрицы 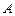 .
.
21. 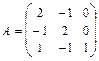 . 22.
. 22. 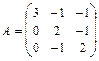 . 23.
. 23. 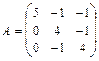 .
.
24. 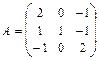 . 25.
. 25. 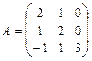 . 26.
. 26. 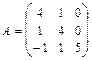 .
.
27. 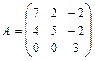 . 28.
. 28. 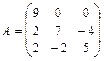 . 29.
. 29. 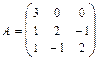 .
.
30. 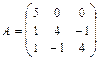 .
.
31 – 40. Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера;
б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
31. 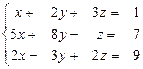 32.
32. 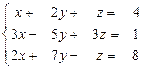
33. 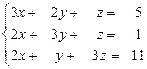 34.
34. 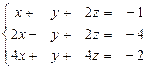
35. 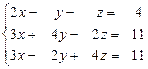 36.
36. 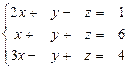
37. 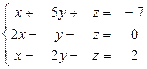 38.
38. 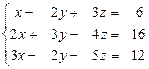
39. 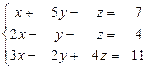 40.
40. 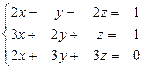
41–50. Найти общее решение системы методом Гаусса:
41. 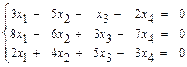 42.
42. 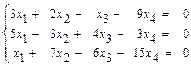
43. 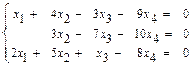 44.
44. 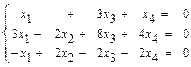
45. 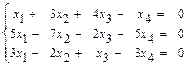 46.
46. 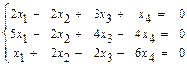
47. 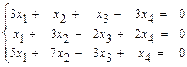 48.
48. 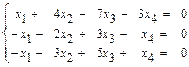
49. 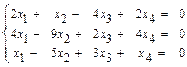 50.
50. 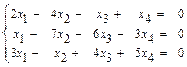
51–60. Найти общее решение системы методом Гаусса:
51. 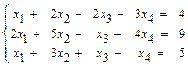 52.
52. 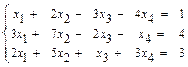
53. 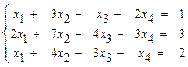 54.
54. 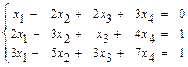
55. 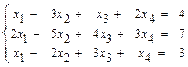 56.
56. 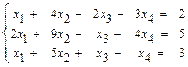
57. 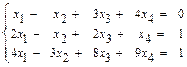 58.
58. 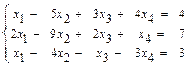
59. 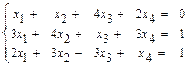 60.
60. 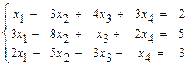
61 – 70. Исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра).
61. 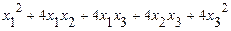 .
.
62. 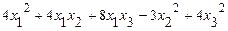 .
.
63. 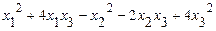 .
.
64. 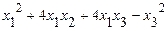 .
.
65. 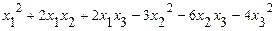 .
.
66. 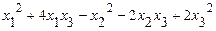 .
.
67. 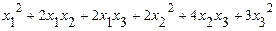 .
.
68. 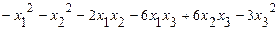 .
.
69. 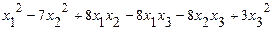 .
.
70. 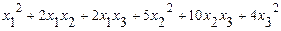 .
.
71 – 80. Даны векторы 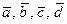 . Требуется:
. Требуется:
а) вычислить скалярное произведение векторов 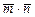 , если
, если 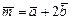 ,
, 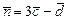 ; б) вычислить векторное произведение векторов
; б) вычислить векторное произведение векторов 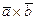 ;
;
в) показать, что векторы 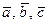 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 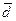 в этом базисе.
в этом базисе.
71. 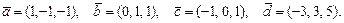
72. 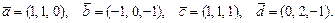
73. 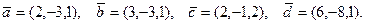
74. 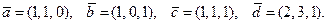
75. 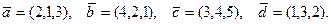
76. 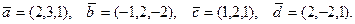
77. 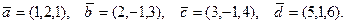
78. 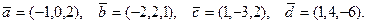
79. 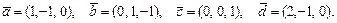
80. 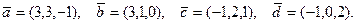
81-90. Даны вершины треугольника 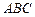 . Требуется найти:
. Требуется найти:
а) длину стороны 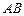 ; б) уравнение стороны
; б) уравнение стороны 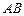 ;
;
в) уравнение медианы 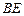 , проведённой из вершины
, проведённой из вершины 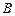 ;
;
г) уравнение высоты 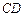 , проведённой из вершины
, проведённой из вершины 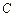 ;
;
д) длину 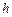 высоты
высоты 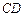 ; е) площадь
; е) площадь 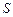 треугольника
треугольника 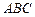 . Сделать чертёж.
. Сделать чертёж.
81. 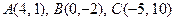 . 82.
. 82. 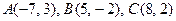
83. 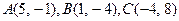 84.
84. 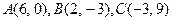
85. 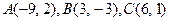 86.
86. 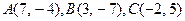
87. 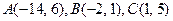 88.
88. 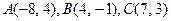
89. 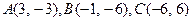 90.
90. 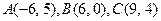
91 – 100. Даны вершины пирамиды 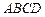 . Требуется найти:
. Требуется найти:
а) длины ребер 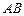 и
и 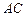 ; б) угол между ребрами
; б) угол между ребрами 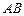 и
и 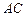 ;
;
в) площадь грани 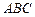 ; г) объем пирамиды
; г) объем пирамиды 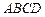 ;
;
д) уравнение плоскости грани 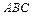 ;
;
е) длину 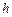 высоты
высоты 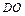 пирамиды
пирамиды 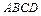 .
.
91. 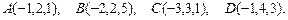
92. 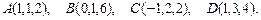
93. 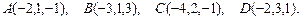
94. 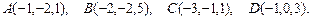
95. 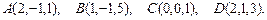
96. 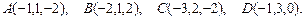
97. 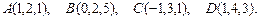
98. 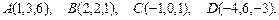
99. 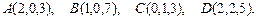
100. 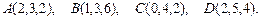
101–110. Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её.
101. 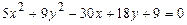 102.
102. 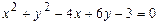
103. 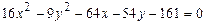 104.
104. 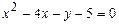
105. 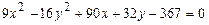 106.
106. 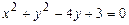
107. 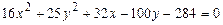 108.
108. 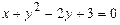
109. 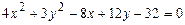 110.
110. 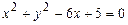
111-120. Требуется: а) изобразить графически область допустимых решений системы неравенств; б) найти графическим способом решение задачи линейного программирования.
111. 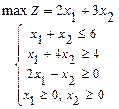 112.
112. 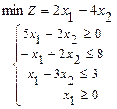 113.
113. 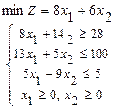
114. 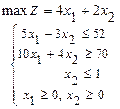 115.
115. 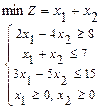 116.
116. 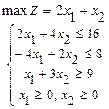
117. 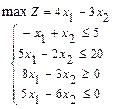 118.
118. 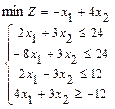
119. 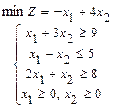 120.
120. 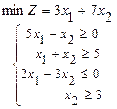
 2015-04-12
2015-04-12 257
257








