а) Длинырёбер 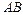 и
и 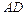 находим как длины векторов
находим как длины векторов 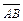 и
и 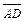 :
:
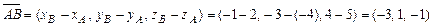 ;
;
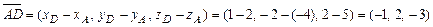 ;
;
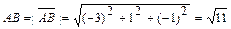 ;
;
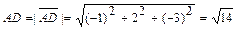 .
.
б) Угол 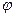 между рёбрами
между рёбрами 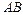 и
и 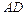 находим как угол между векторами
находим как угол между векторами 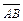 и
и 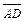 по формуле:
по формуле: 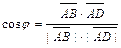 . Учитывая, что:
. Учитывая, что: 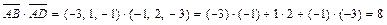 ,
, 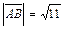 ,
, 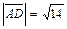 получим
получим 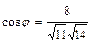 . Откуда
. Откуда 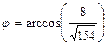
в) Площадь 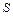 грани
грани 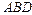 находим, используя геометрический смысл векторного произведения векторов, по формуле
находим, используя геометрический смысл векторного произведения векторов, по формуле 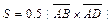 . Учитывая, что:
. Учитывая, что: 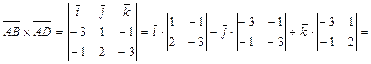
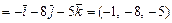 ,
, 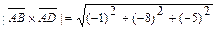 , получим
, получим 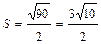 .
.
г) Объём 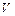 пирамиды
пирамиды 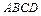 находим, используя геометрический смысл смешанного произведения векторов, по формуле
находим, используя геометрический смысл смешанного произведения векторов, по формуле 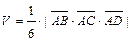 . Учитывая, что:
. Учитывая, что:
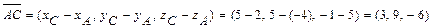 ,
,
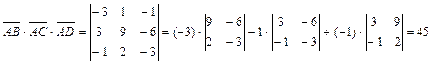 ,
,
получим 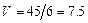 .
.
д) Уравнение плоскости грани 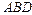 находим как уравнение плоскости, проходящей через точки
находим как уравнение плоскости, проходящей через точки 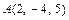 ,
, 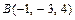 и
и 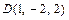 , и записываем его в виде общего уравнения плоскости:
, и записываем его в виде общего уравнения плоскости:
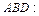
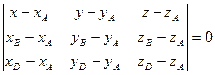
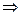
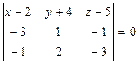
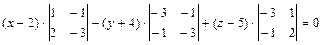
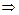
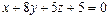
е) Длину 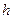 высоты
высоты 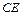 пирамиды
пирамиды 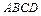 находим как расстояние от точки
находим как расстояние от точки 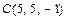 до плоскости
до плоскости 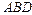 , заданной общим уравнением
, заданной общим уравнением 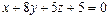 :
:
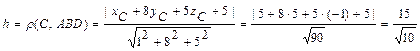 .
.
Ответ: а) 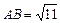 ,
, 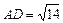 ; б)
; б) 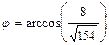 ; в)
; в) 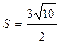 ;
;
г) 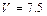 ; д)
; д) 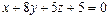 ; е)
; е) 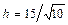 .
.
101–110. Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её:
а) 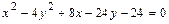 ; б)
; б) 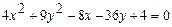 ;
;
в) 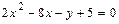 .
.
Решение:
а) Так как 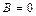 ,
, 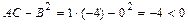 , то уравнение определяет гиперболу с центром в точке
, то уравнение определяет гиперболу с центром в точке 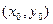 и осями симметрии, параллельными координатным осям:
и осями симметрии, параллельными координатным осям: 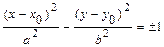 . Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения
. Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения 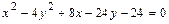 , преобразуем его следующим образом:
, преобразуем его следующим образом:
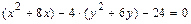
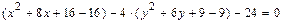
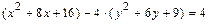
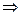
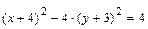
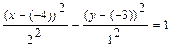 .
.
Полученное уравнение определяет гиперболу с центром в точке 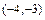 и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат
и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат 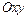 : 1) отмечаем центр гиперболы
: 1) отмечаем центр гиперболы 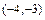 ; 2) проводим через центр
; 2) проводим через центр 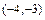 пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром
пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром 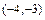 и сторонами
и сторонами 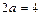 и
и 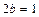 параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
Ответ: Гипербола с центром в точке 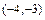 (см. рис.1)..
(см. рис.1)..
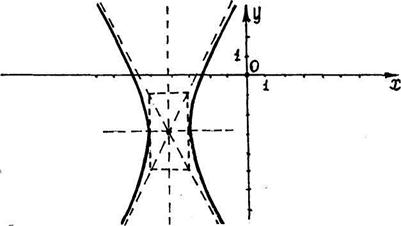
Рис.1
б) Так как 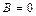 ,
,  ,
, 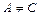 , то уравнение определяет эллипс с центром в точке
, то уравнение определяет эллипс с центром в точке 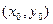 и осями симметрии, параллельными координатным осям:
и осями симметрии, параллельными координатным осям: 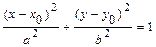 . Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части
. Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части
уравнения 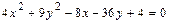 ,преобразуем его следующим образом:
,преобразуем его следующим образом: 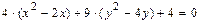
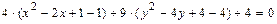
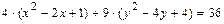
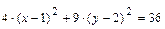
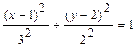 .
.
Полученное уравнение определяет эллипс с центром в точке 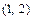 и осями симметрии параллельными осям координат. Для построения эллипса в системе координат
и осями симметрии параллельными осям координат. Для построения эллипса в системе координат  : 1) отмечаем центр эллипса
: 1) отмечаем центр эллипса 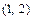 ; 2) проводим через центр
; 2) проводим через центр 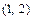 пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром
пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром 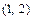 и сторонами
и сторонами 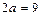 и
и 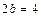 параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
Ответ: Эллипс с центром в точке 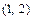 (см. рис.2).
(см. рис.2).
в) Так как 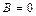 ,
, 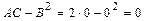 ,
, 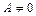 , то уравнение определяет параболу с вершиной в точке
, то уравнение определяет параболу с вершиной в точке 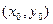 и осью симметрии, параллельной координатной оси
и осью симметрии, параллельной координатной оси 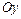 :
: 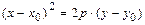 . Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения
. Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения 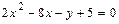 ,преобразуем его следующим образом:
,преобразуем его следующим образом:
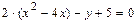
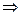
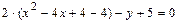
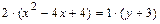
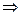
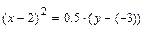
Полученное уравнение определяет параболу с вершиной в точке 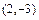 и осью симметрии параллельной оси
и осью симметрии параллельной оси 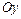 . Для построения параболы в системе координат
. Для построения параболы в системе координат 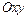 : 1) отмечаем вершину параболы
: 1) отмечаем вершину параболы 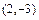 ; 2) проводим через вершину
; 2) проводим через вершину 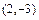 пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы
пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы 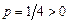 , в положительную сторону оси
, в положительную сторону оси 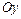 (рис.3).
(рис.3).
Ответ: Парабола с вершиной в точке 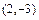 (см. рис.3).
(см. рис.3).
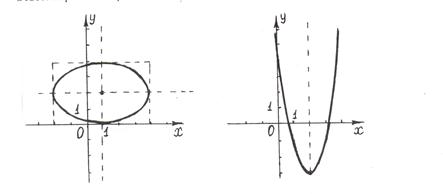
Рис.2. Рис.3.
111-120. Требуется: а) изобразить графически область решений системы неравенств; б) найти графическим способом решение задачи линейного программирования.
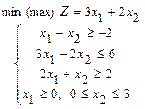
 2015-04-12
2015-04-12 569
569








