1a). Находимвектор
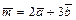
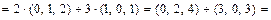
= 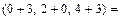
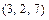 .
.
2а) Находимвектор
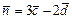
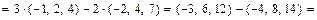
= 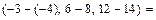
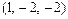 .
.
3а) Вычисляем скалярное произведениевекторов 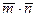 :
:
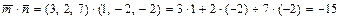 .
.
б) Вычисляем векторное произведение векторов 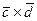 :
:
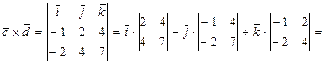
= 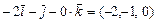
1в) Покажем, что векторы 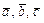 образуют базис
образуют базис 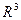 . Для этого составим определитель, столбцами которого являются координаты этих векторов и покажем, что он отличен от нуля.
. Для этого составим определитель, столбцами которого являются координаты этих векторов и покажем, что он отличен от нуля.
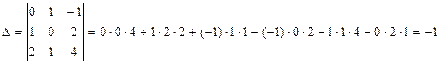 .
.
Так как 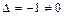 , то векторы
, то векторы 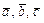 образуют базис
образуют базис 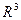 и, следовательно, вектор
и, следовательно, вектор 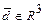 единственным образом можно разложить по векторам этого базиса.
единственным образом можно разложить по векторам этого базиса.
2в) Записываем разложение вектора 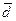 по векторам базиса
по векторам базиса 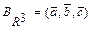 :
:
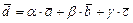 или
или 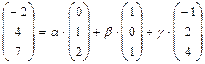 .
.
Коэффициенты разложения 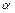 ,
, 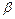 ,
, 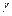 называют координатами вектора
называют координатами вектора 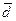 в базисе
в базисе 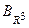 и записывают:
и записывают: 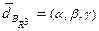 .
.
3в) Записываем векторное уравнение относительно 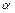 ,
, 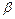 ,
, 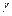 в виде эквивалентной ему системы линейных уравнений:
в виде эквивалентной ему системы линейных уравнений: 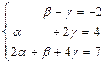 , и находим единственное решение системы, например, по формулам Крамера:
, и находим единственное решение системы, например, по формулам Крамера:
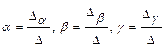 , где
, где
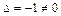 ,
, 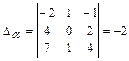 ,
, 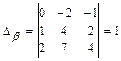 ,
, 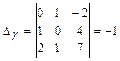 .
.
Таким образом: 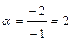 ,
, 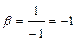 ,
, 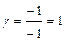 . Следовательно, разложение имеет вид:
. Следовательно, разложение имеет вид: 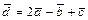 или кратко:
или кратко: 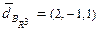 .
.
Ответ: 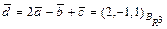 .
.
81-90. Даны вершины треугольника 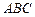 :
: 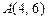 ,
, 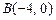 ,
, 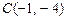 Требуется найти:
Требуется найти:
а) длину стороны 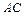 ; б) уравнение стороны
; б) уравнение стороны 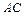 ;
;
в) уравнение медианы 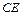 , проведённой из вершины
, проведённой из вершины 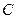 ;
;
г) уравнение высоты 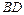 , проведённой из вершины
, проведённой из вершины 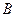 ;
;
д) длину 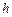 высоты
высоты 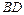 ; е) площадь
; е) площадь 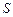 треугольника
треугольника 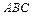 . Сделать чертёж.
. Сделать чертёж.
Решение. Сделаем чертёж:
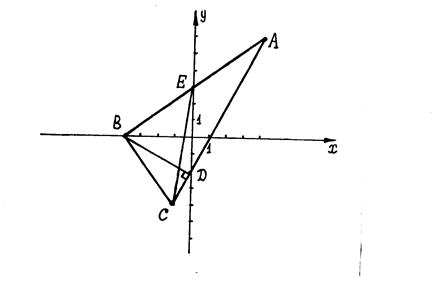
а) Длинустороны 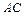 находим как длину вектора
находим как длину вектора 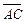 :
:
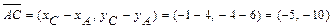 ,
,
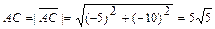 .
.
б) Уравнение стороны 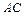 находим как уравнение прямой, проходящей через точки
находим как уравнение прямой, проходящей через точки 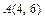 и
и 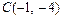 , и записываем его в виде общего уравнения прямой:
, и записываем его в виде общего уравнения прямой:
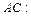
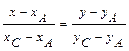
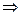
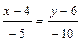
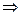
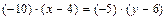
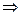
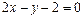 .
.
в) Уравнение медианы 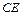 находим как уравнение прямой, проходящей через точки
находим как уравнение прямой, проходящей через точки 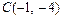 и
и 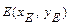 , и записываем его в виде общего уравнения прямой. Неизвестные координаты точки
, и записываем его в виде общего уравнения прямой. Неизвестные координаты точки 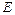 находим как координаты точки, делящей сторону
находим как координаты точки, делящей сторону 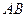 пополам:
пополам:
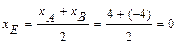 ;
; 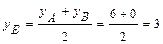 .
.
Тогда: 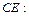
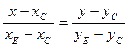
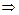
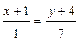
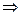
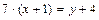
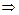
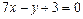 .
.
г) Уравнение высоты 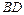 находим как уравнение прямой, проходящей через точку
находим как уравнение прямой, проходящей через точку 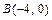 перпендикулярно вектору
перпендикулярно вектору 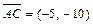 , который принимаем за нормальный вектор прямой
, который принимаем за нормальный вектор прямой 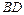 . Тогда
. Тогда 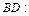
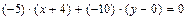
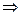
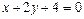
д) Длину 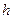 высоты
высоты 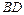 находим как расстояние от точки
находим как расстояние от точки 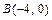 до прямой
до прямой 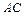 , заданной общим уравнением
, заданной общим уравнением 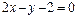 :
:
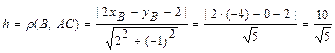 .
.
е) Площадь треугольника 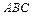 находим по формуле:
находим по формуле: 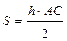 . Откуда
. Откуда 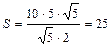 .
.
Ответ: а) 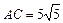 ; б)
; б) 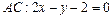 ; в)
; в) 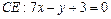 ;
;
г) 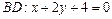 ; д)
; д) 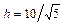 ; е)
; е) 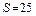 .
.
91 – 100. Даны вершины пирамиды 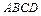 . Требуется найти:
. Требуется найти:
а) длины ребер 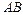 и
и 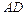 ; б) угол между ребрами
; б) угол между ребрами 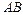 и
и 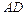 ;
;
в) площадь грани 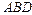 ; г) объем пирамиды
; г) объем пирамиды 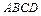 ;
;
д) уравнение плоскости грани 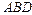 ;
;
е) длину 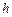 высоты
высоты 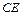 пирамиды
пирамиды 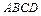 .
.
 2015-04-12
2015-04-12 436
436








