2015-04-12
468
1а) Записываем матрицу квадратичной формы: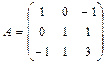 
.
2а) Проверяем является ли матрица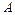 
невырожденной. Для этого вычисляем её определитель 
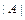и проверяем, равен ли он нулю: 
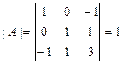. Так как 
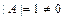, то матрица 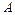- невырожденная и, следовательно, для исследования квадратичной формы на знакоопределённость можно применить критерий Сильвестра.
3а) Вычисляем угловые миноры матрицы 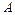и делаем вывод о знакоопределённости квадратичной формы: 
, 
, 
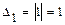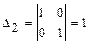. Так как выполняется условие: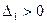 
, 
, 
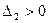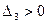, то по критерию Сильвестра квадратичная форма положительно определена.
Ответ: Квадратичная форма положительно определена.
1б) Записываем матрицу квадратичной формы: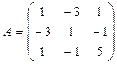 
.
2б) Вычисляем её определитель 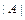и проверяем, равен ли он нулю: 
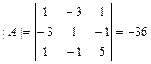. Так как 
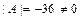, то матрица 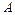- невырожденная и, следовательно, для исследования квадратичной формы на знакоопределённость можно применить критерий Сильвестра.
3б) Вычисляем угловые миноры матрицы 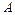и делаем вывод о знакоопределённости квадратичной формы: , 
, 
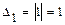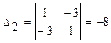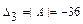. Так как два угловых минора нечётного порядка имеют разные знаки: , 
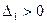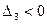, то по критерию Сильвестра квадратичная форма знакопеременна.
|
|
|
Ответ: Квадратичная форма знакопеременна.
71 – 80. Даны векторы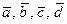 
: 
; 
; 
; 
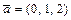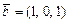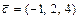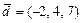. Требуется: а) вычислить скалярное произведение векторов 
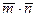, если 
, 
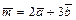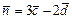; б) вычислить векторное произведение векторов 
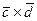; в) показать, что векторы 
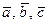образуют базис 
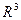и найти координаты вектора 
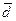в этом базисе.
