Усилия по обеспечению качества изделий проходят четыре фазы. На первой фазе надо просто “делать деталь, как предписано”, причем проверка обычно используется для отбраковки по принципу “годно - не годно”, чтобы удостовериться, что все детали попали внутрь заданных на чертеже границ допуска. Вторая фаза - применение контрольных карт для установления стабильности процессов. Третья фаза - минимизация изменчивости для достижения однородности изделий. Идеи предупреждения дефектов (то есть предотвращение брака в процессе изготовления) и постоянное усовершенствование - часть этой фазы. Четвертая фаза - реализация улучшенной воспроизводимости процесса в более точной настройке средних на оптимальное значение показателя качества изделия или более традиционно – вминимизации затрат (то есть времени сборки). Последняя фаза не менее важна, чем предшествующие. Инженеры-разработчики концентрируются на вопросе “сколь многофункциональное изделие было бы лучше всего” вместо того, чтобы выяснить, сколько характеристик надо учитывать, чтобы изделие могло функционировать. Таким образом, инженеры-производственники должны теперь добиваться требуемого среднего (то есть целевого) значения, а также сохранять низкую изменчивость, чтобы процесс оставался между границами допуска.
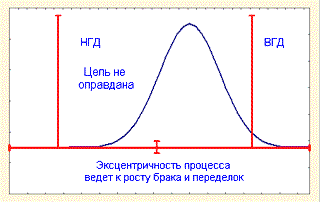
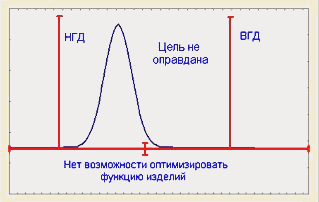
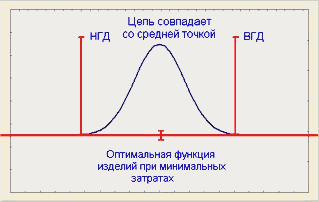
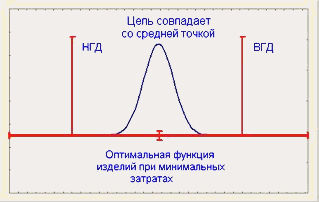
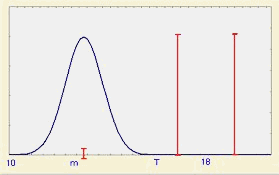
Наиболее распространенное целевое значение, которое применяется на сегодняшний день, - середина между пределами допуска. Это значение часто выбирается как целевое (номинал) для снижения затрат, так как при этом минимизируется вероятность производства бракованного изделия. Сегодня эксцентричные номиналы чаще всего применяются для целенаправленного подбора размеров пар деталей, чтобы облегчить сборку, или для целевого подбора таких размерных цепей на операциях сборки, которые минимизировали бы трудности при проведении разборки. Джессуп (1983) рассматривает применение функции потерь Тагучи, которая ставит в соответствие отклонение от выбранного целевого значения и потери в деньгах. На рис. 7 показано соотношение целевого значения (Т), воспроизводимости процесса и затрат.
 |  |
 |  |
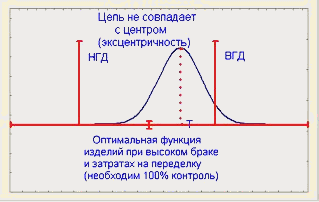 |  |
Рис.7. Воспроизводимость процесса в случае использования целевых значений (номиналов)
Есть множество способов распространения введенных показателей воспроизводимости на случай целевого значения (номинала). Следующее расширение использует аналогию между фактическим и допустимым разбросами процесса, которая показана на рис. 1. Показатель потенциала процесса связывает фактический разброс процесса с допустимым. Из рис. 8 для ближайшего к ВГД значения Т имеем:
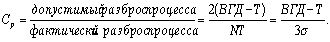
В общем:
 (11)
(11)
Показатель Cp в формуле (11) - обобщение Cp из формулы (1), полученной из отношения допустимого разброса процесса к фактическому. При T=m показатели совпадают.
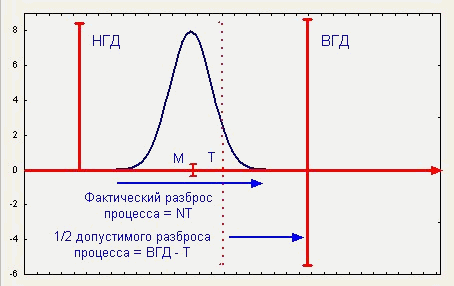
Рис.8. Соотношение параметров Ср при использовании целевых значений
Такую же аналогию можно применить и к показателю k. Из рис. 9 для ближайшего к ВГД значения T, имеем:
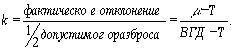
В общем:
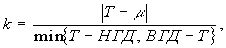 (12)
(12)
где мы предполагаем, что m лежит внутри границ допуска и 0? k? 1. Показатель k в формуле (12) - обобщение показателя k из формулы (9), они эквивалентны при условии T =m. Таким образом индекс Cpk в формуле (10) может применяться при замене Cp и k соответственно на (11) и (12):
Cpk =Min {CPU, CPL}.
где
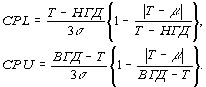
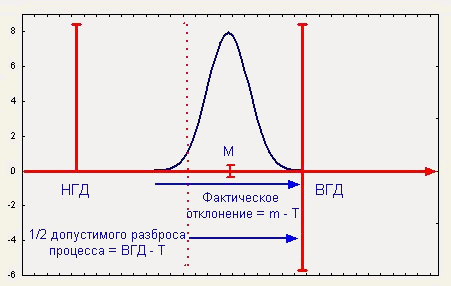
Рис.9. Соотношение параметров К при использовании целевых значений
Обратите внимание, что СPL =0, если | Т -m | > T -НГД, и CPU =0, если | Т -m | >ВГД- T. Эти показатели можно использовать при односторонней границе допуска с целевым значением. Вышеприведенные уравнения аналогичны (8) для Cpk и соответственно CPL и CPU, при условии, что Т =m.
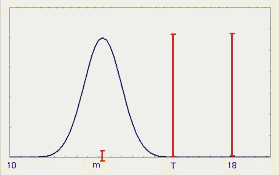
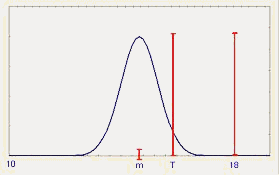
Простой пример иллюстрирует применение этих индексов. Предположим, что ВГД=18, НГД=10, T =16, s =0,67. Обратите внимание, что из формулы (11) Cp =1,0. На рис. 10 представлены индексы воспроизводимости для выбранных значений среднего.
| Распределение | m | CPL | CPU | k | Cpk |
 | |||||
 | |||||
 | |||||
 | |||||
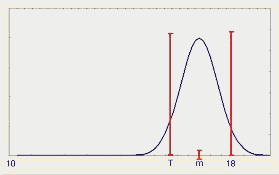 |
Рис.10. Индексы воспроизводимости процесса при целевом значении T=16
Заметьте, что из-за того, что Cpk скорректировано на отклонении от Т, может быть воспроизводимость 0 и не быть ни одной детали за пределами допуска. Таким образом, отклонения в “длинную сторону” (то есть, туда, где расстояние между Т и границей допуска максимально) от целевого значения Т влечет за собой такое же уменьшение Cpk, что и отклонение в “короткую сторону” (то есть туда, где расстояние между Т и границей допуска минимально).
 2015-04-12
2015-04-12 853
853








