Типові практичні завдання

1. Знайти загальний розв’язок неоднорідної системи лінійних рівнянь за методом Гауса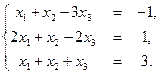

1. Обчислити комплексні корені: .
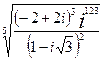2. Знайти ГМТ: .
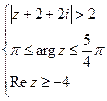3. З’ясувати, чи є вектор 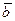лінійною комбінацією векторів ?

.

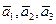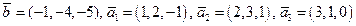1. Знайти ранг системи векторів, базу та подати решту векторів у вигляді лінійної комбінації векторів з цієї бази , .

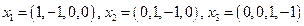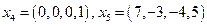6. Обчислити визначник: .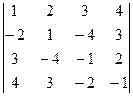

7. Обчислити значення многочлена 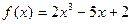від матриці .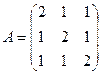

Просто заменить Х на матрицу со всеми вытекающими

8. Знайти обернену матрицю до матриці .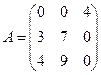

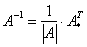
1. Знайти загальний розв’язок неоднорідної системи лінійних рівнянь та фундаментальну систему розв’язків відповідної однорідної СЛР.

.

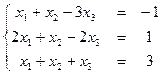1. Знайти ранг матриці в залежності від значення параметру .

.

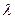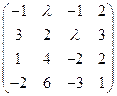1. Знайти найбільший спільний дільник многочленів 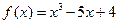і .
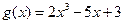2. Визначити кратність кореня 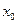многочлена .
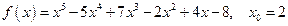3. Відділити кратні корені многочлена
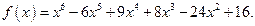
4. Побудувати многочлен найменшого степеня, який має корінь (-1) кратності 2; корені 3, 2- i, I - прості, якщо коефіцієнти цього многочлена – дійсні, комплексні.
5. Найти базисы суммы и пересечения подпространств 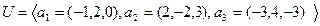та .
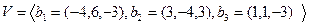6. Доказать, что многочлены 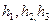создают базис простору 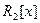, если .

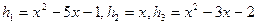17. Доказать, что каждая из двух систем векторов создает базис, и построить матрицу перехода к базису Е к Е´, где

Е: 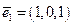, , 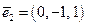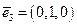; Е´: , , .

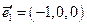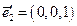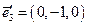1. Рассмотрим плоскость .

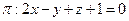- Найти расстояние от 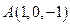к плоскости;

- Составить уравнение плоскости, которая проходит через А параллельно плоскости .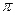

19. Известны координаты вершин тетраэдра .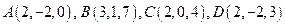
- Вычислить объем тетраэдра
- Составить общее уравнение одной грани и каноническое уравнение одного ребра тетраэдра.
- Вычислить площадь АВС.