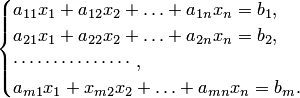2015-04-12
1261
Системой 
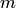линейных алгебраических уравнений с 
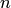неизвестными называется система уравнений вида
Числа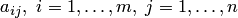 
называются коэффициентами системы; 
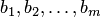— свободными членами, 
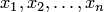— неизвестными. Количество 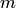уравнений в системе может быть меньше, больше или равно числу 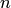неизвестных. Решением системы называется упорядоченная совокупность 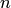чисел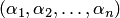 
такая, что после замены неизвестных 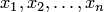соответственно числами 
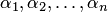каждое уравнение системы превращается в верное числовое равенство. Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.
Систему принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы
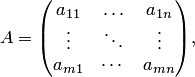
свободные члены записываем в столбец свободных членов
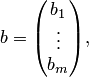
а неизвестные — в столбец неизвестных
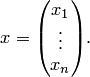
Матричная запись неоднородной системы уравнений (5.1) имеет вид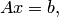 
а однородной: 
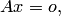где символ 
в правой части обозначает нулевой столбец размеров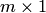 
.
Правило Крамера. Если определитель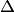 
матрицы системы 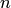линейных уравнений с 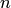неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам
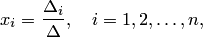где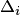 
— определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, т.е.
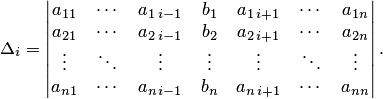
В самом деле, рассмотрим систему (5.6) как матричное уравнение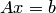 
. Так как определитель 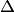матрицы 
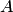отличен от нуля, по теореме 4.2 заключаем, что матричное уравнение 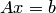имеет единственное решение: 
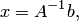где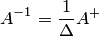 
— обратная матрица. Запишем i-й элемент столбца 
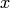, учитывая, что в i-й строке присоединенной матрицы 
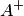стоят алгебраические дополнения i-го столбца матрицы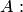 
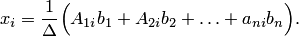
Заметим, что в скобках записано разложение определителя 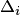по i-му столбцу, т.е. 
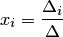, что и требовалось доказать.
