2015-04-12
829
1.Составить расширенную матрицу системы:
2. Используя элементарные преобразования над строками матрицы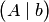 
, привести ее к ступенчатому виду. Если базисный минор матрицы 
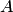расположен в первых 
строках и столбцах, получится следующий вид:
3. Выяснить, совместна система или нет. Для этого определить ранги матриц 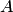и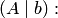 
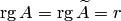— число ненулевых строк в матрице 
;
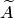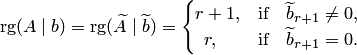
Если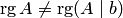 
(при 
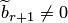), то система не имеет решений. Процесс решения завершен. Если 
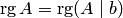(при 
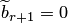), то система совместна. Процесс решения продолжается.
4. Для совместной системы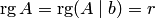 
привести матрицу 
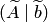к упрощенному виду. Для этого при помощи элементарных преобразований над строками добиваемся того, чтобы в каждом столбце, входящем в базисный минор, все элементы были равны нулю, за исключением одного, равного единице. Если базисный минор матрицы 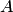расположен в первых строках и первых столбцах, то матрица приводится к упрощенному виду:
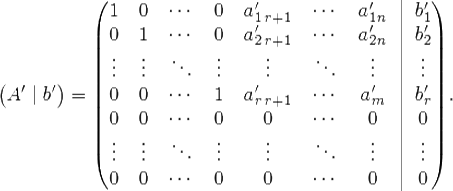
Первые Четыре пункта составляют прямой ход метода Гаусса. Далее применяется обратный метод Гаусса
