Линейно зависимая и линейно независимая система векторов. Их свойства. База пространства и ранг системы векторов

Определение. Векторы 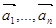называются линейно зависимыми, если существует такая линейная комбинация 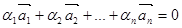, при не равных нулю одновременно a_i, т.е. .

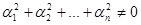Если же только при a_i = 0 выполняется 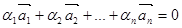, то векторы называются линейно независимыми.

Свойство 1. Если среди векторов 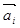есть нулевой вектор, то эти векторы линейно зависимы.

Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

Свойство 6. Любые 4 вектора линейно зависимы.

ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ — частный случай по отношению к общему понятию линейной зависимости. Рассмотрим в качестве примера два произвольных ненулевых вектора, a и b, принадлежащих векторному пространству V.

Если можно подобрать такие не равные нулю числа α и β, что αa + βb = 0, то векторы a и b называются линейно зависимыми. Причина этого ясна: с помощью полученного равенства можно выразить, напр., вектор a через вектор b. Это значит, что a зависит от b. Можно обобщить это определение и на произвольное число векторов: если существуют такие отличные от нуля числа α1,..., αn, что ∑αiai = 0, то векторы называются линейно зависимыми, если же такая система чисел отсутствует, то линейно независимыми.

БАЗИС ВЕКТОРНОГО ПРОСТРАНСТВА — набор из максимального (для данного пространства) числа линейно независимых векторов (см. Линейная зависимость векторов). Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называется ортонормированным. Единичный базисный вектор называют ортом (обозначается ei, где i — номер координаты).

Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = ∑aiei. Коэффициенты разложения ai однозначно определяют вектор a. Поэтому часто говорят, что n-мерный вектор — это упорядоченная совокупность n чисел {ai}. (См. Вектор.) Размерность векторного пространства равна количеству векторов, составляющих его базис.