Формула для вычисления расстояния между точками

В декартовой системе координат

Обозначения:

Eⁿ при n = 1 - прямая, n = 2 - плоскость, n = 3 - пространство;

Rⁿ = 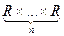(здесь n = 1,2,3) - множество упорядоченных наборов из n действительных чисел;

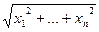|| || = , где Î Rⁿ и = (x₁, …, x_n);

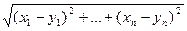|| - || = (*), где , 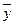Î Rⁿ и = (x₁, …, x_n), 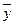= (y₁, …, y_n);

в случае n = 1 || - 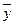|| = |x - y|.

Заметим, что функция f(, 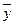) = || - 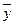|| удовлетворяет требованиям 1-3 из определения меры (см. § …)

Пусть в пространстве Eⁿ введена декартова система координат.

Теорема. Расстояние между точками A и B можно вычислить по следующей формуле:

|AB| = || _A - _B||,

где _A - координаты точки A, _B - координаты точки B.